Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis: Buck Regulators

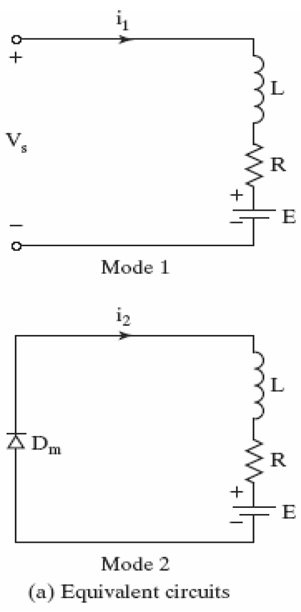
Two modes:

1. Mode 1: switch closed

2. Mode 2: switch open

Power Electronic Converter: Buck Regulators

Mode 1: switch closed, i=i₁

${V_s} = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

Mode 2: switch open, i=i₂

$0 = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

Power Electronic Converter: Buck Regulators-mode

Mode 1:

For i=i₁

${V_s} = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

${V_s} - E = R{i_1} + L\frac{{d{i_1}}}{{dt}}$

Laplace Transform

$\frac{{{V_s} - E}}{s} = R{I_1}(s) + Ls{I_1}(s)$

$\frac{{{V_s} - E + Ls{i_1}(0)}}{s} = {I_1}(s)(R + Ls)$

${I_1}(s) = \frac{{{V_s} - E + Ls{i_1}(0)}}{{s(R + Ls)}}$

Partial Fraction Expansion

${I_1}(s) = \frac{{{V_s} - E + Ls{i_1}(0)}}{{s(R + Ls)}} = \frac{{{V_s} - E + Ls{i_1}(0)}}{{sL(s + R/L)}}$

$= \frac{{\frac{{{V_s}}}{L} - \frac{E}{L} + s{i_1}(0)}}{{s(s + R/L)}}$

$= \frac{{{V_s} - E}}{{sR}} - \frac{{{V_s} - E - R{i_1}(0)}}{{R(s + R/L)}}$

Inverse Laplace Transform

${i_1}(t) = \frac{{{V_s} - E}}{R} - \frac{{{V_s} - E}}{R}{e^{ - tR/L}} + {i_1}(0){e^{ - tR/L}}$

Rearrange to get-

${i_1}(t) = {i_1}(0){e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

Use initial cdt: I₁=i₁(0)

${i_1}(t) = {I_1}{e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

Design features of Buck Regulator

Good design requires load time constant > switching time and τ=L/R > T
τ : time required to reach 63.2% of final value.
When τ<T, we see the full exponential change in i
When τ>T, we see just a part of the exponential change in i before the switch, and so we assume that I increases/decreases linearly between switching times
Ex: T=.001sec; L=7.5mH, R=5Ω and τ=L/R=.0015sec

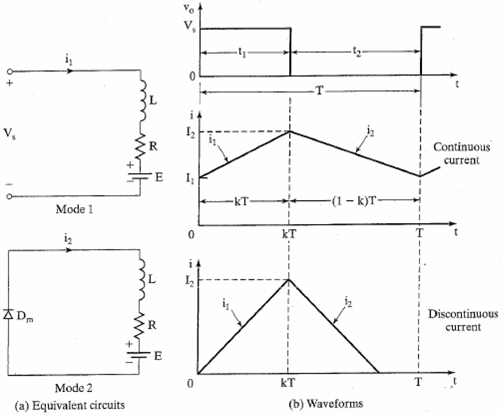
Equivalent circuits and waveforms

Figure: Equivalent circuits and waveforms for RL loads.

But what is I1, I2?

Let’s look at previous equations for i₁ and i₂

From Mode 1 current expression & “boundary” condition at switching

${i_1}(t) = {I_1}{e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

We have

${i_1}(t = {t_1} = kT) \equiv {I_2}$

$\Rightarrow {I_2} = {i_1}(t = kT) = {I_1}{e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$ (5.15)

From Mode 2 current expression & “boundary” condition at switching

${i_2}(t) = {I_2}{e^{ - tR/L}} - \frac{E}{R}(1 - {e^{ - tR/L}})$

We have ${i_2}(t = {t_2}) = {I_3}$ and also note ${t_2} = (1 - k)T$

$\Rightarrow {I_3} = {i_2}(t = (1 - k)T) = {I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})$ (5.16)

From previous elastration, observe that, in steady-state, I₃=I₁….

$\Rightarrow {I_1} = {i_2}(t = (1 - k)T) = {I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})$ (5.16a)

Substitute (5.16a) into (5.15):

${I_2} = {i_1}(t = kT) = \left( {{I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})} \right){e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

Now solve for I₂

${I_2} = {I_2}{e^{ - (1 - k)TR/L}}{e^{ - kTR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}}){e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

$= {I_2}{e^{ - TR/L}} - \frac{E}{R}({e^{ - kTR/L}} - {e^{ - TR/L}}) + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

$\Rightarrow {I_2}(1 - {e^{ - TR/L}}) = - \frac{E}{R}({e^{ - kTR/L}} - {e^{ - TR/L}}) + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

${I_2} = - \frac{E}{R}\frac{{({e^{ - kTR/L}} - {e^{ - TR/L}})}}{{(1 - {e^{ - TR/L}})}} + \frac{{{V_s} - E}}{R}\frac{{(1 - {e^{ - kTR/L}})}}{{(1 - {e^{ - TR/L}})}}$

${I_2} = \frac{{[ - E{e^{ - kTR/L}} + E{e^{ - TR/L}} + {V_s} - E - {V_s}{e^{ - kTR/L}} + E{e^{ - kTR/L}}]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{\left[ {E{e^{ - TR/L}} + {V_s} - E - {V_s}{e^{ - kTR/L}}} \right]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{\left[ { - E(1 - {e^{ - TR/L}}) + {V_s}(1 - {e^{ - kTR/L}})} \right]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{{E(1 - {e^{ - TR/L}})}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{E}{R}$

${I_2} = \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{E}{R}$ (5.18)

Substitute eq. 5.18 into 5.16a:

${{I_1} = \left[ {\frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R}} \right]{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})}$

$= \frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}}{e^{ - (1 - k)TR/L}} - \frac{E}{R}{e^{ - (1 - k)TR/L}} - \frac{E}{R} + \frac{E}{R}{e^{ - (1 - k)TR/L}})$

$= \frac{{{V_s}({e^{ - TR/L}} - {e^{ - (1 - k)TR/L}})}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R}$

$= \frac{{{V_s}(1 - {e^{kTR/L}})}}{{R(1 - {e^{TR/L}})}} - \frac{E}{R}$

$= \frac{{{V_s}({e^{kTR/L}} - 1)}}{{R({e^{TR/L}} - 1)}} - \frac{E}{R}$

Summary-

Define z=TR/L

${I_2} = \frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R} \Leftarrow Eq.5.18 \Rightarrow {I_2} = \frac{{{V_s}({e^{ - kz}} - 1)}}{{R({e^{ - z}} - 1)}} - \frac{E}{R}$

${I_1} = \frac{{{V_s}({e^{kTR/L}} - 1)}}{{R({e^{TR/L}} - 1)}} - \frac{E}{R} \Leftarrow Eq.5.17 \Rightarrow {I_1} = \frac{{{V_s}({e^{kz}} - 1)}}{{R({e^z} - 1)}} - \frac{E}{R}$

What is z?

Recall τ =L/R is the time constant.
$\Rightarrow z = T/\tau$
So z is the ratio of chopping (or switching) period to load time constant.
Now let’s consider the peak-to-peak ripple current.

Figure: Equivalent circuits and waveforms for RL loads.

Therefore the peak-to-peak ripple current is given by

$\Delta I = {I_2} - {I_1}$

Plug in eq. 5.17 and 5.18 and will get:

$\Delta I = \frac{{{V_s}}}{R}\frac{{1 - {e^{ - kz}} + {e^{ - z}} - {e^{ - (1 - k)z}}}}{{1 - {e^{ - z}}}} - \frac{E}{R}......Eq.5.19$

It is interesting to identify the duty ratio for maximum ripple. To do this, differentiate eq 5.19 with respect to k and set to 0.

$\frac{d}{{dk}}\Delta I = \frac{d}{{dk}}\left\{ {\frac{{{V_s}}}{R}\frac{{1 - {e^{ - kz}} + {e^{ - z}} - {e^{ - (1 - k)z}}}}{{1 - {e^{ - z}}}} - \frac{E}{R}} \right\} = 0$