PWM Inverters

Pulse Width Modulation (PWM)
  1. The amplitude of the harmonics can be reduced by using the pulse width modulation (PWM) technique.
  2. The basic concept of the PWM method is the division of the on-time into several on and off periods with varying duration.
  3. The rms value of the ac voltage is controlled by the on-time of the switches.
  4. The most frequently used PWM technique is sinusoidal pulse width modulation (SPWM).
Types of Pulse Width Modulation (PWM)
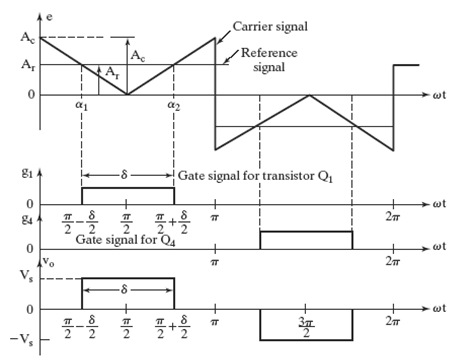
    1. Single-pulse-width modulation
    2. Multiple-pulse-width modulation
    3. Sinusoidal pulse-width modulation
    4. Modified sinusoidal pulse-width modulation
    5. Phase-displacement control
    Single-Pulse PWM
    Duty ratio D is given by
    \begin{array}{l} D = \frac{\delta }{\pi }\\ or\\ \delta = D\pi \end{array}
    Pulse duration
    D = \frac{\delta }{\omega } = {t_2} - {t_1}
          = M{T_S} = M\frac{T}{2}
    {v_o}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{n\delta }}{2}\sin n\omega t}
    {v_{o(rms)}} = \sqrt {\frac{2}{{2\pi }}\int_{(\pi - \delta /2)}^{(\pi + \delta /2)} {V_S^2d\theta } } = {V_S}\sqrt {\frac{\delta }{\pi }}


    power-electronic-converter-Single-Pulse PWM

    Harmonic Profile for p =1
    power-electronic-converter-Single-Pulse PWM
    Example 1
    A pulse width modulated single phase full-bridge inverter has a dc input of 240V. The inverter is operating at a duty cycle of 60% with a frequency of 5kHz. Determine-
    1. the rms value of the ac output voltage,                       [185.9V]
    2. the rms value of the fundamental frequency component of the output ac voltage                                                  [174.74V]
    3. the rms value of the total harmonic component of the output voltage.                                                                 [63.44V]
    Example 2
    A full-bridge PWM inverter operates from a 200V dc bus. The instantaneous output voltage v can be expressed using Fourier series as
    v = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{nD\pi }}{2}\cos n(\omega t - \frac{{D\pi }}{2})}
    Determine
    1. The duty cycle that will totally eliminate the third harmonic. [D = 2/3]
    2. What will be the rms values of the total output voltage and the fundamental frequency voltage as well as THD at the duty cycle in (a).                               [Vrms = 163.3V, V1,rms = 155.88V]
    previous Single-Phase Bridge Inverter
    next Multiple-Pulse PWM

    No comments:

    Post a Comment

    Please wait for approval of your comment .......