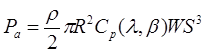Presentation on EFFECTS OF PARAMETERS VARIATION ON WIND POWER GENERATION
Objectives
Output power equation of wind turbine
Output power, P=0.5ρAV3Cp
Where,
ρ= Air density, kg/m3
A=Rotor swept area, m2
V=Wind velocity, m/s
Cp=Power co-efficient
Cp vs. λ equation
Cp = 0.5 (116/λi -0.4α -5) e-21/λi
Where,
λi = {1/ (λ+0.08 α) -0.035/ (α3+1)}-1
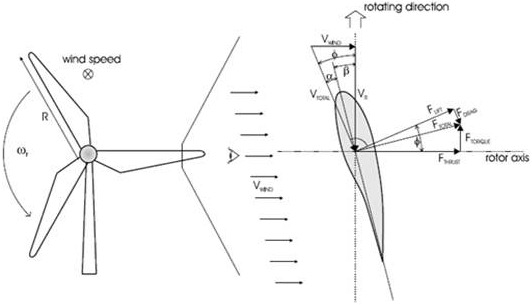
λ = ωm R / υ
λ =Tip speed ratio
α = Blade angle
Factors affecting the wind power generation
Cp vs. λ (TSR) curve for different blade angle (α) for V52 model

3D view of power coefficient (Cp) for V52 model

Swept area variation for V52 model

Air density variation for V52 model

Aerodynamic power variation as a function of (Cp) for V52 model

Cp vs. λ curve for different blade angle (α) for V80 model

3D view of power coefficient (Cp) for V80 model

Swept area variation for V80 model
Air density variation for V80 model

Aerodynamic power variation as a function of (Cp) for V80 model

Cp vs. λ curve for different blade angle (α) for V90 model

3D view of power coefficient (Cp) for V90 model

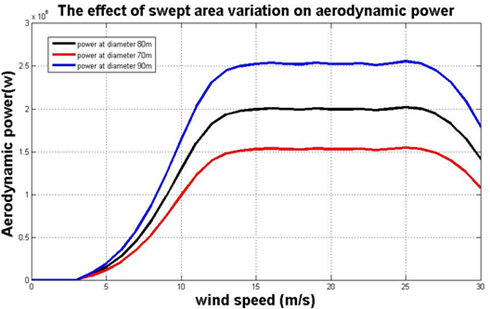
Swept area variation for V90 model

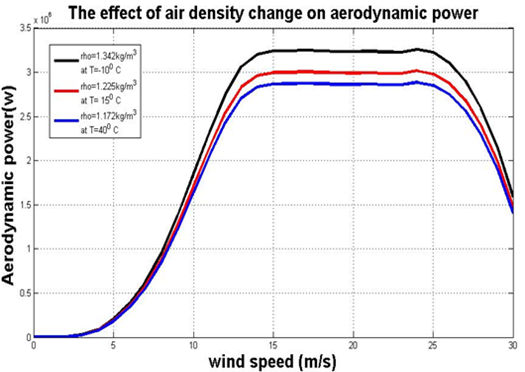
Air density variation for V90 model
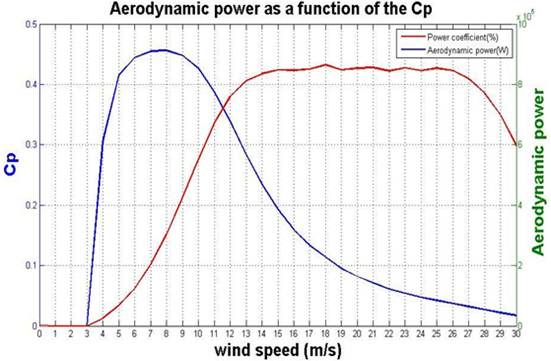
Aerodynamic power variation as a function of (Cp) for V90 model
 Conclusion
Conclusion
Objectives
- To analysis the effects of different parameters variation on wind power generation
- To analysis the Cp vs. λ curve of wind turbine model
- To observe the 2D and 3D view of Cp vs. λ curve for different wind turbine model.
Output power equation of wind turbine
Output power, P=0.5ρAV3Cp
Where,
ρ= Air density, kg/m3
A=Rotor swept area, m2
V=Wind velocity, m/s
Cp=Power co-efficient
Cp vs. λ equation
Cp = 0.5 (116/λi -0.4α -5) e-21/λi
Where,
λi = {1/ (λ+0.08 α) -0.035/ (α3+1)}-1
λ = ωm R / υ
λ =Tip speed ratio
α = Blade angle
Factors affecting the wind power generation
- The windiness of the site
- Availability
- Seasonal and diurnal variation of wind power
- Effect of height
- Wind velocity variation with time
- Wind turbine arrangement
- Wind velocity (V)
- Turbine swept area (A)
- Air density(ρ)
- Power coefficient (Cp)
- Wind velocity has a cubic relation with wind power generation
- Wind speed varies for different reasons-
height,Three design speed
season,
day night effect etc.
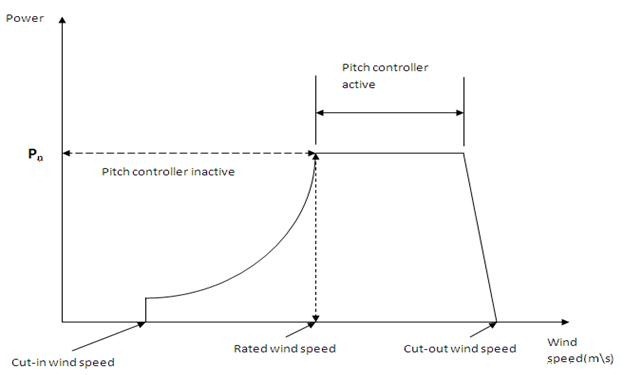
- Cut in speed, Vc = (0.6 to 0.7) Vm
- Rated speed, Vr =(1.5 to2.0) Vm
- Furling (Cut off) speed, Vf =≥3 Vm
- The swept area of wind turbine’s blades is a function of rotor diameter.
- The power output of a wind turbine is directly related to the swept area.
- If double the swept area, the amount of energy which can capture by the wind turbine will be double.
- Air density is one of the factors that affects the wind turbine power generation.
- Air density is effected by-
TemperaturePower coefficient (cp)
Pressure
Elevation
- Power coefficient (Cp) is the percentage of power available in the wind that is converted into mechanical power.
- It is a function of blade angle (α), and the tip-speed-ratio, (λ).
- Maximum value of Cp is 0.593 but wind turbine rotors achieve values 0.4 to 0.5 due to different loss.

Cp vs. λ (TSR) curve for different blade angle (α) for V52 model

3D view of power coefficient (Cp) for V52 model

Swept area variation for V52 model

Air density variation for V52 model

Aerodynamic power variation as a function of (Cp) for V52 model

Cp vs. λ curve for different blade angle (α) for V80 model

3D view of power coefficient (Cp) for V80 model

Swept area variation for V80 model

Air density variation for V80 model

Aerodynamic power variation as a function of (Cp) for V80 model

Cp vs. λ curve for different blade angle (α) for V90 model

3D view of power coefficient (Cp) for V90 model

Swept area variation for V90 model

Air density variation for V90 model

Aerodynamic power variation as a function of (Cp) for V90 model
 Conclusion
Conclusion- From the Simulation result it can be seen that the output power is directly related to wind speed ,swept area, air density and Cp.
- Output power mainly affected by the swept area.
- Output power of same wind turbine varies due to change in air density but it has a small effect.
- Output power is a function Cp
- Cp is a function of blade angle & tip speed ratio.
- Cp is maximum when blade angle is minimum.