previous Basic Tutorials in Finite Element Analysis Using MSC/ PATRAN and MSC/ NASTRAN
SM = Subordinate Menu. This referees to the menus that pop up from options selected in the right menu.
From the TM choose File
In the resulting pull down menu choose New Database
A SM called New Database pops up
Turn off (button up) Modify Preferences
Under New Database Name enter truss.db
Click OK
A menu called New Model Preferences will appear
Select Tolerance to be based on the model
Set Model Dimension = 2.0
Analysis code = MSC/Nastran
Analysis Type = structural
Click OK
From the TM choose Load/BC's
A RM called Load/Boundary Conditions will appear
Set Action = Create
Object = Displacement
Type = Nodal
Set Current Load Case = Default
Enter New Set Name as leftfix
( This is for the clamping of the left most bottom nodes)
Click Input Data...
a SM appears
Set Load/BC Scale Factor = 1.
Set Translations to <0,0,0>
Leave the Rotations blank
Be sure Analysis Coordinate Frame is Coord0
Click OK
(back in the Load/Boundary Conditions RM)
Click Select Application Region
a SM called Select Application Region appears with a Select menu on its left edge.
In the Select Application Region SM Turn on the Geometry (button down)
Click in box under Select Geometric Entities
In the Select Menu (which is just to the left of the SM) Click on the picture with a point
In the main view port, click on point 1 (left most point on the bottom edge)
A Selection Choices menu will appear. Choose Point 1.
( This will cause the words "Point 1" to appear in the Select Geometric Entities box in the RM)
Click on Add just below this box
( This will remove the words "Point 1" from the Select Geometric Entities box and add them to the Application Region box)
Click OK
(The Load / Boundary Condition RM appears again)
Click Apply
change Action = Create
Object = Force
Type = Nodal
Change the New Set Name to topload
Click Input Data...
a SM appears
Enter the force vector <0 , -100 , 0>
leave the moments < > (i.e. blank)
Click OK
From the TM choose Elements
A RM appears called Finite Elements
Set Action = Create
Object = Mesh Seed
Type = Uniform
Select Number of Elements (button down)
Number = 1
Turn off the Auto Execute (button up)
Click in Curves List box
Click on curve 1 in the main viewport
(curve 1 is the line between point 1 and point 2. This is the bottom left part of the truss)
(The words "Curve 1" will be added to the Curve List)
Click Apply
(circles which represent finite element nodes will appear on points 1 and 2)
Do the same for curves 2-9.
(The nodes created above must now be tied together with elements)
(up at the top of the RM)
Set Action = Create
Object = Mesh
Type = Curve
Click on Bar2 under Element Topology Click Curve List Box
Click curve 1 in the main viewport
Click Apply
Do the same for curves 2-9
To see the element numbers on the truss, click the “Label Control” button (Looks like an “L”) on the top row menu. This adds a label control tool bar which allows you to turn on/off labels for different geometric and/or finite element entities.
(up at the top of the RM)
Set Action = Equivalence
Object = All
Type = Tolerance Cube
(The purpose here is to tie the nodes together that lie on top of one another)
Leave the Nodes to be Excluded list blank
Set the Equivalencing Tolerance to .001
Click Apply
(The command window at the bottom of the PATRAN desktop will tell you that 12 nodes were deleted)
6. The materials are specified next: On the TM select Materials
a RM will appear called Materials
Set Action = Create
Object = Isotropic
Method = Manual Input
Click Material Name box
Input the name to be Aluminum
Click Input Properties box
SM called Input Options appears
Input Elastic Modulus = 7.0E10
Input Poisson = 0.3
OK
Back in the Materials RM
Click Apply
(The Existing Materials box should have Aluminum in it)
Click Add (The words Element 1:9 appears in the Application Region box)
Click Apply in the Element Properties menu
(truss1 will be added to the Existing Property Sets box)
8. The analysis is to be done is specified next:
On the TM select Analysis a RM will appear called Analysis
Set Action = Analyze
Object = Entire Model
Method = Full Run
Click on Solution Type a SM will appear
Click on Translation Parameters A SM called Translation Parameters will appear
Set Data Output to OP2 and Print
Click OK
Back in the Analysis RM
Set Solution Type = Static (button down)
Click OK
(back in the RM Analysis)
Click Apply
(The analysis will take a few seconds to run)
On the TM select File
From the pull down menu select Quit
next MODELING A CANTILEVERED BEAM WITH END LOAD USING 4 NODE SHELL ELEMENTS
MSC Patran Tutorial # 2
Modeling of a Truss
I. THE PHYSICAL PROBLEM:
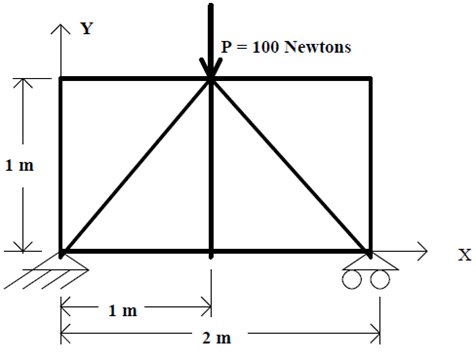
The truss structure shown below has nine members. Each of the members is made of aluminum and each has the same cross sectional area. The lower left corner of the structure is constrained in all three directions. The lower right hand corner is constrained in the Y and Z directions, but is free to roll in the X direction. A vertical load of 100 Newtons is applied at the midpoint of the top of the truss. The loading is directed downward. The truss geometry is symmetric about the vertical line through the point at which the force is applied. Material properties, as well as physical dimensions, are given below.
The truss structure shown below has nine members. Each of the members is made of aluminum and each has the same cross sectional area. The lower left corner of the structure is constrained in all three directions. The lower right hand corner is constrained in the Y and Z directions, but is free to roll in the X direction. A vertical load of 100 Newtons is applied at the midpoint of the top of the truss. The loading is directed downward. The truss geometry is symmetric about the vertical line through the point at which the force is applied. Material properties, as well as physical dimensions, are given below.
For the truss below:
Young's modulus = 70 x 109 N/ (m2 ) (Aluminum)
Poisson's ratio = 0.3
Truss members are (3 cm X 3 cm) square
Young's modulus = 70 x 109 N/ (m2 ) (Aluminum)
Poisson's ratio = 0.3
Truss members are (3 cm X 3 cm) square

II. THINKING ABOUT THE MECHANICS
Before you begin the computational model of the structure, study the structure for a few minutes to determine if it has any peculiarities. Ask a few introductory questions:
I. Is the truss constrained from any rigid body displacements or rotations?
II. What direction do you expect the reactions to be in?
III. What magnitudes should the directions have?
IV. Are there any “zero-force” members in the truss?
V. Use the method of sections (or another method if you prefer) to analytically determine the stresses in a few of the members.
Before you begin the computational model of the structure, study the structure for a few minutes to determine if it has any peculiarities. Ask a few introductory questions:
I. Is the truss constrained from any rigid body displacements or rotations?
II. What direction do you expect the reactions to be in?
III. What magnitudes should the directions have?
IV. Are there any “zero-force” members in the truss?
V. Use the method of sections (or another method if you prefer) to analytically determine the stresses in a few of the members.
III. THE GEOMETRIC AND FINITE ELEMENT MODEL
In the modeling instructions below, the geometry is specified by creating the MSC/Patran geometric entity called a "curve" between each of the truss’s joints. In this manner, each truss member becomes a separate curve in the geometric portion of the database. The lengths and directions of the curves correspond to those of the members in the physical truss structure.
In the modeling instructions below, the geometry is specified by creating the MSC/Patran geometric entity called a "curve" between each of the truss’s joints. In this manner, each truss member becomes a separate curve in the geometric portion of the database. The lengths and directions of the curves correspond to those of the members in the physical truss structure.
Each of the truss members is modeled using a single 2-node rod element. Each element is originally created with two unique nodes which no other element shares. The procedure called "equivalencing" in MSC/PATRAN creates a single node from two or more nodes which have the same physical location. Therefore, after equivalencing, there are nine elements and six nodes in this structure. These elements have three displacement degrees of freedom per node. The elements can only model axial (membrane) deformations. Bending type deformations, which are evidenced by rotation of the element cross section, are not accounted for by this particular element. Torsion of the members is also neglected. The neglect of torsion and bending are very common assumptions in truss problems, as these are higher order effects in a great number of truss type structures. Physically, this non-bending assumption is representative of pinned joints (for 2-D) or spherical joints (for 3-D). It should be noted, however, that there are some situations where these assumptions would not allow your model to correctly capture the physics of the problem. This type of modeling assumption should be carefully considered.
The loading is modeled with a single concentrated force of magnitude 100 on the center node of the top of the structure. It is also possible to position loads on geometric entities like points and surfaces instead of on finite element entities like nodes. This is demonstrated in other tutorials. The boundary conditions are established by constraining the displacements at the lower left node to be zero in all 3 directions and the lower right node to be zero in the Y and Z directions. Material properties and lengths are input corresponding to the figure of the truss above. Note that it is not necessary to carefully number the nodes of the structure for minimization of the bandwidth of the stiffness matrix. The code automatically renumbers the nodes for bandwidth minimization before solving the system of equations.
IV. THE FINITE ELEMENT THEORY
The finite elements used to model two and three dimensional truss structures are actually just the simple 2-node bar elements spatially extrapolated to function in two or three dimensional space. This spatial extrapolation is in the form of a transformation of the axial direction of the arbitrarily oriented bar into the global (fixed) coordinate system. The results of the transformation is found in the following stiffness matrix for the two dimensional case.
The finite elements used to model two and three dimensional truss structures are actually just the simple 2-node bar elements spatially extrapolated to function in two or three dimensional space. This spatial extrapolation is in the form of a transformation of the axial direction of the arbitrarily oriented bar into the global (fixed) coordinate system. The results of the transformation is found in the following stiffness matrix for the two dimensional case.
where the order of the degrees of freedom is {u1 , v1 , u2 , v2}. The A, E, and L are the cross sectional area, Young's (elastic) modulus and axial length respectively. The c and s in the matrix stand for Cos (θ) and Sin (θ) respectively. The orientation of the bar and the angle θ are shown below.
This element does not have any stiffness associated with rotational degrees of freedom. Therefore, bending and torsion effects are not included in this model nor is it possible to load the structure with moments. Also, the element, in the manner it is used in this analysis, does not have the ability to model large deformations and will not warn the user in case of buckling type failures (i.e. geometric nonlinearities). Similarly, this type of analysis does not have the ability to correctly model stresses which are not in the elastic range of the material (i.e. material nonlinearities).
V. STEP BY STEP INSTRUCTIONS FOR BUILDING THE TRUSS MODEL USING PATRAN
Preliminaries for using MSC/PATRAN include:
Preliminaries for using MSC/PATRAN include:
- Log on to the computer
- Change to the directory that you wish to contain your analysis results
3) Left click START (lower left corner of the NT desktop), go to PROGRAMS, then top MSC (common), then to MSC Patran 90. This will bring up the MSC/Patran Program.
In the instructions below, the following abbreviations and terms will be used:
TM = Top Menu. This refers to the horizontal menu options residing at the top of the screen after PATRAN has been initiated.
RM = Right Menu. This refers to the menus that pop up after an option has been chosen from the top menu. These menus reside on the far right side of the PATRAN desktop.SM = Subordinate Menu. This referees to the menus that pop up from options selected in the right menu.
Click = Unless otherwise stated, this indicates a click with the left mouse button.
Boldface will indicate text that occurs in the PATRAN menus.
Italics text will indicate text that you must enter into text boxes in the PATRAN menus or text that you choose in a menu scroll box.
1. Our first step is to create a new database: From the TM choose File
In the resulting pull down menu choose New Database
A SM called New Database pops up
Turn off (button up) Modify Preferences
Under New Database Name enter truss.db
Click OK
A menu called New Model Preferences will appear
Select Tolerance to be based on the model
Set Model Dimension = 2.0
Analysis code = MSC/Nastran
Analysis Type = structural
Click OK
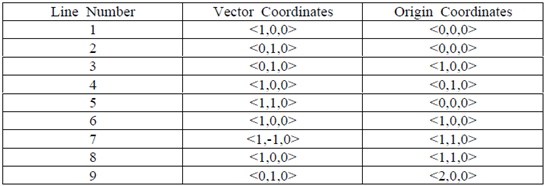
2. The geometry of the truss will be determined next: From the TM choose Geometry
A RM called Geometry will result
Set Action = Create
Object = Curve
Method = XYZ
Set the Curve ID list to 1
Set Reference Coordinate Frame to Coord 0
Turn off the Auto Execute button (uncheck)
Enter the following into the Vector Coordinates list:
<1,0,0>
Enter the following into the Origin Coordinates list:
<0,0,0>
(note that PATRAN will accept either commas or blanks as separators between coordinates)
Click Apply
Build the rest of the truss using the following tableA RM called Geometry will result
Set Action = Create
Object = Curve
Method = XYZ
Set the Curve ID list to 1
Set Reference Coordinate Frame to Coord 0
Turn off the Auto Execute button (uncheck)
Enter the following into the Vector Coordinates list:
<1,0,0>
Enter the following into the Origin Coordinates list:
<0,0,0>
(note that PATRAN will accept either commas or blanks as separators between coordinates)
Click Apply

Note that the commands Construct, Line, XYZ do NOT work based on the coordinates of the 2 end points of the truss member. These commands generate lines based on the origin and the vector for that particular truss member.
Note that if you make a mistake you can erase by clicking on the undo button on the top of the PATRAN desktop. This will erase the LAST CONSTRUCTION COMMAND ONLY. In other words, it will take the process back to before you hit the Apply button the last time.
3. The boundary conditions are specified next: From the TM choose Load/BC's
A RM called Load/Boundary Conditions will appear
Set Action = Create
Object = Displacement
Type = Nodal
Set Current Load Case = Default
Enter New Set Name as leftfix
( This is for the clamping of the left most bottom nodes)
Click Input Data...
a SM appears
Set Load/BC Scale Factor = 1.
Set Translations to <0,0,0>
Leave the Rotations blank
Be sure Analysis Coordinate Frame is Coord0
Click OK
(back in the Load/Boundary Conditions RM)
Click Select Application Region
a SM called Select Application Region appears with a Select menu on its left edge.
In the Select Application Region SM Turn on the Geometry (button down)
Click in box under Select Geometric Entities
In the Select Menu (which is just to the left of the SM) Click on the picture with a point
In the main view port, click on point 1 (left most point on the bottom edge)
A Selection Choices menu will appear. Choose Point 1.
( This will cause the words "Point 1" to appear in the Select Geometric Entities box in the RM)
Click on Add just below this box
( This will remove the words "Point 1" from the Select Geometric Entities box and add them to the Application Region box)
Click OK
(The Load / Boundary Condition RM appears again)
Click Apply
(3 displacement constraint arrows and the numbers 1,2,3 should now appear in the main viewport window on the extreme right point on the bottom of the truss)
Back in the RM called Load/Boundary Conditions Set Action = Create
Object = Displacement
Type = Nodal
Set Current Load Case = Default
Enter New Set Name as rightfix
( This is for the clamping of the right most bottom nodes)
Click Input Data...
a SM appears
Set Load/BC Scale Factor = 1.
Set Translations to < ,0,0>
Note the space left in before the first comma in the Translations vector. This ensures that the X direction is NOT constrained
Leave the Rotations blank
Be sure Analysis Coordinate Frame is Coord0
Click OK
(back in the Load/Boundary Conditions RM)
Click Select Application Region
a SM called Select Application Region appears with a Select
menu on its left edge.
In the Select Application Region SM
Turn on the Geometry (button down)
Click in box under Select Geometric Entities
In the Select Menu (which is just to the left of the SM)
Click on the picture with a point
In the main view port, click on point 5 (right most point on the bottom edge)
A Selection Choices menu will appear. Choose Point 5.
( This will cause the words "Point 5" to appear in the Select Geometric Entities box in the RM)
Click on Add just below this box
( This will remove the words "Point 5" from the Select Geometric
Entities box and add them to the Application Region box)
Click OK
(The Load / Boundary Condition RM appears again)
Click Apply
Object = Displacement
Type = Nodal
Set Current Load Case = Default
Enter New Set Name as rightfix
( This is for the clamping of the right most bottom nodes)
Click Input Data...
a SM appears
Set Load/BC Scale Factor = 1.
Set Translations to < ,0,0>
Note the space left in before the first comma in the Translations vector. This ensures that the X direction is NOT constrained
Leave the Rotations blank
Be sure Analysis Coordinate Frame is Coord0
Click OK
(back in the Load/Boundary Conditions RM)
Click Select Application Region
a SM called Select Application Region appears with a Select
menu on its left edge.
In the Select Application Region SM
Turn on the Geometry (button down)
Click in box under Select Geometric Entities
In the Select Menu (which is just to the left of the SM)
Click on the picture with a point
In the main view port, click on point 5 (right most point on the bottom edge)
A Selection Choices menu will appear. Choose Point 5.
( This will cause the words "Point 5" to appear in the Select Geometric Entities box in the RM)
Click on Add just below this box
( This will remove the words "Point 5" from the Select Geometric
Entities box and add them to the Application Region box)
Click OK
(The Load / Boundary Condition RM appears again)
Click Apply
(2 displacement constraint arrows and the numbers 2,3 should now appear in the main viewport window on the extreme right point on the bottom of the truss)
4. The loads are specified next: (Continuing on in the Load/BC's RM) change Action = Create
Object = Force
Type = Nodal
Change the New Set Name to topload
Click Input Data...
a SM appears
Enter the force vector <0 , -100 , 0>
leave the moments < > (i.e. blank)
Click OK
(Continuing on in the Load/BC's RM)
Click Select Application Region
A SM called Select Application Region appears with a select menu just to its left
In the Select Application Region menu
Select the Geometry Filter = Geometry
Click in the Select Geometry Entities box
In the select menu to the left of the SM Click on the point icon
In the main viewport, click on the point 4 (top center point) (point 4 will be added to the Select Geometric Entities list)
In the Select Application Region menu
Click Add
(Point 4 will be added to the Application Region list)
Click OK
(Load/BC's menu now reappears)
Click Apply
(A vector with the load of magnitude 100 in the –Y direction will appear on point 4 in the main viewport)
5. The finite element mesh is specified next: Click Select Application Region
A SM called Select Application Region appears with a select menu just to its left
In the Select Application Region menu
Select the Geometry Filter = Geometry
Click in the Select Geometry Entities box
In the select menu to the left of the SM Click on the point icon
In the main viewport, click on the point 4 (top center point) (point 4 will be added to the Select Geometric Entities list)
In the Select Application Region menu
Click Add
(Point 4 will be added to the Application Region list)
Click OK
(Load/BC's menu now reappears)
Click Apply
(A vector with the load of magnitude 100 in the –Y direction will appear on point 4 in the main viewport)
From the TM choose Elements
A RM appears called Finite Elements
Set Action = Create
Object = Mesh Seed
Type = Uniform
Select Number of Elements (button down)
Number = 1
Turn off the Auto Execute (button up)
Click in Curves List box
Click on curve 1 in the main viewport
(curve 1 is the line between point 1 and point 2. This is the bottom left part of the truss)
(The words "Curve 1" will be added to the Curve List)
Click Apply
(circles which represent finite element nodes will appear on points 1 and 2)
Do the same for curves 2-9.
(The nodes created above must now be tied together with elements)
(up at the top of the RM)
Set Action = Create
Object = Mesh
Type = Curve
Click on Bar2 under Element Topology Click Curve List Box
Click curve 1 in the main viewport
Click Apply
Do the same for curves 2-9
To see the element numbers on the truss, click the “Label Control” button (Looks like an “L”) on the top row menu. This adds a label control tool bar which allows you to turn on/off labels for different geometric and/or finite element entities.
(up at the top of the RM)
Set Action = Equivalence
Object = All
Type = Tolerance Cube
(The purpose here is to tie the nodes together that lie on top of one another)
Leave the Nodes to be Excluded list blank
Set the Equivalencing Tolerance to .001
Click Apply
(The command window at the bottom of the PATRAN desktop will tell you that 12 nodes were deleted)
6. The materials are specified next: On the TM select Materials
a RM will appear called Materials
Set Action = Create
Object = Isotropic
Method = Manual Input
Click Material Name box
Input the name to be Aluminum
Click Input Properties box
SM called Input Options appears
Input Elastic Modulus = 7.0E10
Input Poisson = 0.3
OK
Back in the Materials RM
Click Apply
(The Existing Materials box should have Aluminum in it)
7. The properties for each element are assigned next: On the TM select Element Properties
a RM will appear called Element Properties
Set Action = Create
Dimension = 1d
Type = Rod
Click Property Set Name box
Enter truss1
Click Input Properties a SM appears called Input Properties Click in the Material Name box
Click on the word "Aluminum" in the Materials Property Set box
( the words m:Aluminum will appear in the Material Name box)
Click in the Area box
Enter .0009 (recall that the member’s cross section was 3cm x
3cm square)
Click OK
Back in the Element Properties RM)
Click Select Members box
In the select menu just to the left of the SM
Click in the box which contains finite element with 2 end nodes (This allows you to pick finite element entities as opposed to the geometric entities in the other box)
a RM will appear called Element Properties
Set Action = Create
Dimension = 1d
Type = Rod
Click Property Set Name box
Enter truss1
Click Input Properties a SM appears called Input Properties Click in the Material Name box
Click on the word "Aluminum" in the Materials Property Set box
( the words m:Aluminum will appear in the Material Name box)
Click in the Area box
Enter .0009 (recall that the member’s cross section was 3cm x
3cm square)
Click OK
Back in the Element Properties RM)
Click Select Members box
In the select menu just to the left of the SM
Click in the box which contains finite element with 2 end nodes (This allows you to pick finite element entities as opposed to the geometric entities in the other box)
Move the cursor arrow to a point to the left and above the highest, leftmost point on the truss. Click and hold down the left mouse button. Drag the cursor (while holding down the mouse button) to a point to the right of and below the right-most bottom node. A "selection box" is formed while you drag. Release the button.
(The words Elm 1:9 will appear in the Select Members box) Click Add (The words Element 1:9 appears in the Application Region box)
Click Apply in the Element Properties menu
(truss1 will be added to the Existing Property Sets box)
8. The analysis is to be done is specified next:
On the TM select Analysis a RM will appear called Analysis
Set Action = Analyze
Object = Entire Model
Method = Full Run
Click on Solution Type a SM will appear
Click on Translation Parameters A SM called Translation Parameters will appear
Set Data Output to OP2 and Print
Click OK
Back in the Analysis RM
Set Solution Type = Static (button down)
Click OK
(back in the RM Analysis)
Click Apply
(The analysis will take a few seconds to run)
Now we’ll read the results into the graphics database (back in the RM Analysis)
Set Action = Read Output2
Object = Result Entities
Method = Translate
Click on Select Results File
Choose truss.op2 (you may need to go to the root or home directory to find this. If this file does not exist, then there was an error in your model. Go to the file truss.log or truss.f06 to attempt to find out what error occurred.)
Back in the Analysis RM
Click Apply
Set Action = Read Output2
Object = Result Entities
Method = Translate
Click on Select Results File
Choose truss.op2 (you may need to go to the root or home directory to find this. If this file does not exist, then there was an error in your model. Go to the file truss.log or truss.f06 to attempt to find out what error occurred.)
Back in the Analysis RM
Click Apply
9. Visualize the results
From the TM choose Results A RM called Results appears
Set Action = Create
Object = Quick Plot
Under Select Fringe Result Choose Displacements, Translational
Set Quantity = Y Component
Under Select Deformation Results, choose Displacements, Translational
Click Apply ( A deformed plot appears with colors indicating the level of deformation. Note that the visual deformation of the truss is magnified so that you can see the deformation “mode”. The actual truss deformations are very small; as can be seen by the numerical values, which are NOT scaled)
Note that you can also view the stress results in this manner. Simply choose Stress, Tensor from the Select Fringe Result options. Recall that there are a number of ways to compute and extrapolate the stresses for a bar and these will make significant differences in the values which are plotted.
From the TM choose Results A RM called Results appears
Set Action = Create
Object = Quick Plot
Under Select Fringe Result Choose Displacements, Translational
Set Quantity = Y Component
Under Select Deformation Results, choose Displacements, Translational
Click Apply ( A deformed plot appears with colors indicating the level of deformation. Note that the visual deformation of the truss is magnified so that you can see the deformation “mode”. The actual truss deformations are very small; as can be seen by the numerical values, which are NOT scaled)
Note that you can also view the stress results in this manner. Simply choose Stress, Tensor from the Select Fringe Result options. Recall that there are a number of ways to compute and extrapolate the stresses for a bar and these will make significant differences in the values which are plotted.
10. Check the written report of the truss results.
The file containing the written results from the analysis is scaled truss.f06. Open the file (by simply double clicking on it). The file might be in the root or home directory or in the directory from which you ran the analysis.
The file containing the written results from the analysis is scaled truss.f06. Open the file (by simply double clicking on it). The file might be in the root or home directory or in the directory from which you ran the analysis.
In this file find the displacement vectors and record the numerical values. These will help you answer some of the question below. Also, find the vectors for the stresses and constraint forces and record these values.
Next you will end your MSC PATRAN session by saving your database and exiting On the TM select File From the pull down menu select SaveOn the TM select File
From the pull down menu select Quit
next MODELING A CANTILEVERED BEAM WITH END LOAD USING 4 NODE SHELL ELEMENTS


No comments:
Post a Comment
Please wait for approval of your comment .......