In this section we will examine in detail the single-phase full-bridge VSC. Its power circuit is shown in Figure 6.26. It consists of two identical legs like the half-bridge single-phase converter (Figure 6.23) discussed in Section 6.3.1. Specifically, there are four switching elements (S1, S2, S3, S4), four antiparallel diodes (D1, D2, D3, D4) and a DC bus voltage source Vdc that can be a single capacitor. The other leg provides the return path for the current this time and the DC bus mid-point does not need to be available to connect the load. The output voltage v0 appears across the two points A and B as shown in Figure 6.26.
The control restriction discussed for the single-phase half-bridge topology (Figure 6.23) applies to this converter as well. Clearly the control signals for the switch pairs (S1, S2) and (S3, S4) must be complementary to avoid any bridge destruction due to shoot through of infinite current (at least theoretically).
There are two control methods for this topology. The first one treats the switches (S1, S4) and (S2, S3) as a pair. This means that they are turned on and off at the same time and for the same duration. For square-wave operation the switches S1 and S4 are on for half of the period. For the other half, the pair of S2, S3 is turned on. Like the single-phase half-bridge VSC, the direction of the output current i0 determines the conduction state of each semiconductor.
When the two switches S1 and S4 are turned on, the voltage at the output is equal to the DC bus voltage Vdc. Similarly, when the switches S2 and S3 are turned on the output voltage is equal to - Vdc. Such circuit operation is illustrated in Figure 6.27.
In the first case, when the direction of the output current io is positive as shown in Figure 6.26, the current flows through switches S1 and S4 and the power is transferred from the DC side to the AC one (t4 < t < t5). When the current becomes negative, although the switches S1 and S4 are turned on, the diodes D1 and D4 conduct the current and return power back to the DC bus from the AC side (t3 < t < t4). For the other half of the period, when the switches S2 and S3 are turned on and the current is positive, the diodes D2 and D3 conduct (t1 < t < t2). In this
Fig. 6.26 Single-phase full-bridge VSC.
Fig. 6.27 Key waveforms of the single-phase full-bridge VSC circuit operation. (a) output voltage V0 = VAB; (b) output current i0; (c) input DC bus current id; (d) harmonic spectrum of the output voltage V0 = VAB; (e) harmonic spectrum of the output current i0; and (f) harmonic spectrum of the input DC bus current id.
instance, power is transferred also back to the DC side from the AC side. Finally, when the current is negative, the switches S2 and S3 carry the current and assist the converter to transfer power from the DC bus to the AC side (t2 < t < t3). In summary, there are four distinct modes of operation for this converter when the control method shown in Figure 6.27 is employed (two inverter modes and two rectifier modes). Simply said, at all times two switches are turned on and the legs are controlled in a synchronized way.
The output voltage v0 = vAB is shown in Figure 6.27(a). The output current i0 and the input DC current id are also plotted in Figures 6.27(b) and (c) respectively. Similarly, like the case of the half-bridge topology, the square-wave generated across the AC side includes all odd harmonics and being a single-phase system, the third harmonic is also present (Figure 6.27(d)). These harmonics when reflected back to the DC side source include all even harmonics (Figure 6.27(f).
Fig. 6.28 Quadrants of operation of the single-phase full-bridge VSC.
The fundamental component of the output voltage v0 waveform has an amplitude value of
(6.20)
And its various harmonics are given by
where h is the order of the harmonic.
The converter is capable of operating in all four quadrants of voltage and current as shown in Figure 6.28. The various modes and their relationship to the switching and/or conduction state of the semiconductors are also summarized in Table 6.4 for further clarity. The phase relationship between the AC output voltage and AC output current does not have to be fixed and the converter can provide real and reactive power at all leading and lagging power factors. However, the converter itself cannot control the output voltage if the DC bus voltage Vdc remains constant. There is a need to adjust the level of the DC bus voltage if one wants to control the rms value of the output voltage v0.
There is however a way to control the rms value of the fundamental component of the output voltage as well as the harmonic content of the fixed waveform shown in Figure 6.27(a). In this method, the control signals of the two legs are not
Table 6.4 Modes of operation of the single-phase full-bridge VSC
synchronized in any way and the switches are not treated as pairs like previously. For the safe operation of the converter, the control signals between (S1 and S2) and (S3 and S4) must be complementary. In this case, there is a phase- shift between the two legs and this way a zero volts interval can appear across the output.
For instance, if switches S1 and S3 are turned on at the same time, the output voltage (vAB) will be zero. The current in the case of other than unity power factor must keep flowing. There is no power exchange between the DC side and the AC one (free-wheeling mode). If the current is positive, the current flows through S1 and D3. If the current is negative, it flows through D1 and S3. Similarly, when the two bottom switches S2 and S4 are turned on at the same time, the output voltage (vAB) is zero and the output current once again determines which element conducts and allows the output current to continue flowing. Specifically, if the current is positive, the diode D2 and the switch S4 are conducting. In the case that the current is negative, the switch S2 and diode D4 provide a path for the output current. These extra modes of operation for the single-phase full-bridge topology (Figure 6.26) are also included in Table 6.4 as the free-wheeling modes.
For a given phase-shift (a degrees) between the control signals of the two legs, the waveforms are shown in Figure 6.29. It is clear that the output voltage waveform is a three-level one, being able to have the values of Vdc, 0 and -Vdc as shown in Figure 6.29(a). The control signals are shown in Figures 6.29(b)-(d). It is also clear that between the top and bottom switches of each leg complementary control signals are used. It should be noted that for α = 0, the output voltage becomes similar to the previously presented control method (square-wave, Figure 6.27(a)).
The output voltage vo (vAB) is shown in Figure 6.30(a) along with the output current io and the DC bus current id in Figures 6.30(b) and (c) respectively. Therefore, by controlling the phase-shift between the two legs (α degrees), the rms value of the fundamental component can be controlled. The amplitude of all odd harmonics, as shown in Figure 6.30(d) for the output voltage, can also be controlled. The output current has only a fundamental component as shown in Figure 6.30(e), where the DC bus current has a DC component and all even harmonics as shown in Figure 6.30(f).
Fig. 6.29 Key waveforms of the single-phase full-bridge phase-shifted controlled VSC circuit operation. (a) output voltage vo = vAB; (b) control signal for switch S1 ; (c) control signal for switch S2; (d) control signal for switch S3; and (e) control signal for switch S4.
Fig. 6.30 Key waveforms of the single-phase full-bridge phase-shifted controlled VSC circuit operation. (a) output voltage vo = vAB; (b) output current io; (c) DC bus current id; (d) harmonic spectrum of the output voltage vo = vAB; (e) harmonic spectrum of the output current io; and (f) harmonic spectrum of the input DC bus current id.
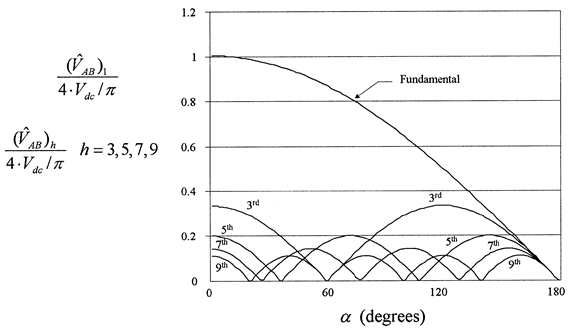
Fig. 6.31 Normalized amplitudes of fundamental and harmonics for the phase-shifted output voltage as a function of α (zero volts interval in degrees).
For a given zero interval α in degrees, as shown in Figures 6.29(a) and 6.30(a), the amplitude of the fundamental and harmonics are as follows
where h is the order of the harmonic.
When α = 0 the converter operates as a square-wave one (Figure 6.27). The normalized amplitude of the fundamental and the most significant harmonics, i.e. 3rd, 5th, 7th and 9th to the output of the square-wave converter as a function of α, are plotted in Figure 6.31.
previous Single-phase half-bridge VSC
next Conventional three-phase six-step VSC















0 comments:
Post a Comment
Please wait for approval of your comment .......