Wound Rotor Induction Generators (WRIGs): Steady State
Wound rotor induction generators (WRIGs) are provided with three phase windings on the rotor and on the stator. They may be supplied with energy at both rotor and stator terminals. This is why they are called doubly fed induction generators (DFIGs) or double output induction generators (DOIGs). Both motoring and generating operation modes are feasible, provided the power electronics converter that supplies the rotor circuits via slip-rings and brushes is capable of handling power in both directions. As a generator, the WRIG provides constant (or controlled) voltage Vs and frequency f1 power through the stator, while the rotor is supplied through a static power converter at variable voltage Vr and frequency f2.
The rotor circuit may absorb or deliver electric power. As the number of poles of both stator and rotor windings is the same, at steady state, according to the frequency theorem, the speed ωm is as follows:
(1.1)
where
is the number of pole pairs
is the mechanical rotor speed
FIGURE 1.1 Wound rotor induction generator (WRIG) main operation modes: (a) basic configuration, (b) subsynchronous generating (ωr < ω1), (c) supersynchronous generating (ωr > ω1), and (d) rotor output WRIG (brushless exciter).
The sign is positive (+) in Equation 1.1 when the phase sequence in the rotor is the same as in the stator and ωm < ω1, that is, subsynchronous operation. The negative (−) sign in Equation 1.1 corresponds to an inverse phase sequence in the rotor when ωm > ω1, that is, supersynchronous operation.
For constant frequency output, the rotor frequency ω2 has to be modified in step with the speed variation. This way, variable speed at constant frequency (and voltage) may be maintained by controlling the voltage, frequency, and phase sequence in the rotor circuit.
It may be argued that the WRIG works as a synchronous generator (SG) with three-phase alternating current (AC) excitation at slip (rotor) frequency ω2 = ω1 − ωm. However, as ω1 ≠ ωm, the stator induces voltages in the rotor circuits even at steady state, which is not the case in conventional SGs. Additional power components thus occur.
The main operational modes of WRIG are depicted in Figure 1.1a through Figure 1.1d (basic configuration shown in Figure 1.1a). The first two modes (Figure 1.1b and Figure 1.1c) refer to the already defined subsynchronous and supersynchronous generations. For motoring, the reverse is true for the rotor circuit; also, the stator absorbs active power for motoring. The slip S is defined as follows:
A WRIG works, in general, for ω
2 ≠ 0 (S ≠ 0), the machine retains the characteristics of an induction machine. The main output active power is delivered through the stator, but in supersynchronous operation, a good part, about slip stator powers (SPs), is delivered through the rotor circuit. With limited speed variation range, say from S
max to −S
max, the rotor-side static converter rating — for zero reactive power capability on the rotor side — would be
With S
max typically equal to ±0.2 to 0.25, the static power converter ratings and costs would correspond to 20 to 25% of the stator delivered output power.
At maximum speed, the WRIG will deliver increased electric power, P
max:
(1.3)
with the WRIG designed at Ps for ωm = ω1 speed. The increased power is delivered at higher than rated speed:
(1.4)
Consequently, the WRIG is designed electrically for Ps at ωm = ω1, but mechanically at wmmax and Pmax. The capability of a WRIG to deliver power at variable speed but at constant voltage and frequency represents an asset in providing more flexibility in power conversion and also better stability in frequency and voltage control in the power systems to which such generators are connected.
The reactive power delivery by WRIG depends heavily on the capacity of the rotor-side converter to provide it. When the converter works at unity power delivered on the source side, the reactive power in the machine has to come from the rotor-side converter. However, such a capability is paid for by the increased ratings of the rotor-side converter. As this means increased converter costs, in general, the WRIG is adequate for working at unity power factor at full load on the stator side.
Large reactive power releases to the power system are still to be provided by existing SGs or from WRIGs working at synchronism (S = 0, ω2 = 0) with the back-to-back pulse-width modulated (PWM) voltage converters connected to the rotor controlled adequately for the scope.
Wind and small hydroenergy conversion in units of 1 megawatt (MW) and more per unit require variable speed to tap the maximum of energy reserves and to improve efficiency and stability limits. High-power units in pump-storage hydro- (400 MW [1]) and even thermopower plants with WRIGs provide for extra flexibility for the ever-more stressed distributed power systems of the near future. Even existing (old) SGs may be retrofitted into WRIGs by changing the rotor and its static power converter control.
The WRIGs may also be used to generate power solely on the rotor side for rectifier loads (Figure 1.1d). To control the direct voltage (or direct current [DC]) in the load, the stator voltage is controlled, at constant frequency ω1, by a low-cost alternating current (AC) three-phase voltage changer. As the speed increases, the stator voltage has to be reduced to keep constant the current in the DC load connected to the rotor (ω2 = ω1 + ωm). If the machine has a large number of poles (2p1 = 6,8,12), the stator AC excitation input power becomes rather low, as most of the output electric power comes from the shaft (through motion).
Such a configuration is adequate for brushless exciters needed for synchronous motors (SMs) or for generators, where field current is needed from zero speed, that is, when full-power converters are used in the stator of the respective SMs or SGs.
With 2p1 = 8, n = 1500 rpm, and f1 = 50 Hz, the frequency of the rotor output f2 = f1 + np1 = 50 + (1500/60)∗ 4 = 150 Hz. Such a frequency is practical with standard iron core laminations and reduces the contents in harmonics of the output rectified load current.
In these series of articles, the following subjects related to WRIG steady state will be detailed:
- Construction elements
- Basic principles
- Inductances
- Steady-state model (equations, phasor diagram, equivalent circuits)
- Steady-state characteristics at power grid
- Steady-state characteristics for isolated loads
- Losses and efficiency
Construction Elements
The WRIG topology contains the following main parts:
- Stator laminated core with Ns uniformly distributed slots
- Rotor laminated core with Nr uniformly distributed slots
- Stator three-phase winding placed in insulated slots
- Rotor shaft
- Stator frame with bearings
- Rotor copper slip-rings and stator (placed) brushes to transfer power to (from) rotor windings
- Cooling system
Magnetic Cores
The stator and rotor cores are made of thin (typically 0.5 mm) nonoriented grain silicon steel lamination provided with uniform slots through stamping (Figure 1.2.a). To keep the airgap reasonably small, without incurring large core surface harmonics eddy current losses, only the slots on one side may be open. On the other side of the airgap, they should be half closed or half open (Figure 1.2b).
Though, in general, the use of radial-axial ventilation systems led to the presence of radial channels between 60 and 100 mm long elementary stacks, at least for powers up to 2 to 3 MW, axial ventilation with single lamination stacks is feasible (Figure 1.3a and Figure 1.3b). As the airgap is slightly increased in comparison with standard induction motors, the axial airflow through the airgap is further facilitated. The axial channels (Figure 1.3a) in the stator and rotor yokes (behind the slot region) play a key role in cooling the stator and the rotor, as do the radial channels (Figure 1.3b) for the radial-axial ventilation.
The radial channels, however, are less efficient, as they are “traveled” by the windings, and thus, additional phase resistance and leakage inductance are added by the winding zones in the radial channel contributions. In very large, or long, stack machines, radial-axial cooling may be inevitable, but, as explained before, below 3 MW, the axial cooling in unistack cores, already in industrial use for induction motors, seems to be the way of the future.
FIGURE 1.2 (a) Stator and (b) rotor slotted lamination.
FIGURE 1.3 Stator and rotor stacks: (a) for axial cooling and (b) for radial-axial cooling.
Windings and Their mmfs
The stator and rotor three-phase windings are similar in principle. Later in Synchronous Generators, their design is described in some detail. Here, only the basic issues are presented. The three-phase windings are built to provide for traveling magnetomotive forces (mmfs) capable of producing a traveling magnetic field in the uniform airgap (slot openings are neglected or considered through the Carter coefficient KC = 1.02 to 1.5):
(1.5)
where
is equal to the mmfs per pole produced by either stator or rotor windings g is the airgap
is the Carter coefficient to account for airgap increase due to slot openings
is the iron core contribution to equivalent magnetic reluctance of the main flux path (Figure 1.2a)
To produce a traveling airgap field, the stator and rotor mmfs, seen from the stator and from the rotor, respectively, have to be as follows:
(1.6)
(1.7)
where p1 is the number of electrical periods of the magnetic field wave in the airgap or of pole pairs. The rotor mmf is produced by currents of frequency ω2.
At constant speed, the rotor and stator geometrical angles are related by
where ω
r is the rotor speed in electrical radians per second (rad/sec). Consequently, F
r(θ
s, t) becomes
![{F_r}({\theta _s},t) = {F_1}\cos \left[ {{p_1}{\theta _s} - \left( {{\omega _r} \pm {\omega _2}t} \right) + \gamma } \right]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sRoa6T-nCqoQZ932tRfjOsBTOnKrYlHNk9aXPVH_auZxCK5-L2qPAP_pQnSLYGfUXw2Wq7H76xvuVaJNlGlbLRJeZ32QzUX0gThtUq66waJ0ITIsgXbI-sj5IZI85WgOad65QtnSjJ2NHbG6utc4ed5n0-0jo8PKVgcccRl1oHs1TdQRiYcj3TRITFf4iHim6XjMlEqMivH07tJSYjjHCsXp-twoU4RC3NDypA1zlGFzVl068YyHLDwI201cEsel-Qv1G2iBNMD9ctrYccRBEeVZ9CQqpzAd_0cZV7ZYOZxJGNusgEgviXD-jtMDrwzy87D83iyXpJ_fhOHv606l7QrR7t95usyiWXMw_d08rbpuCiSBWibAG-I5kQSbC8QH7pekSgTq62bub7y0qr02jZGngAYrk=s0-d)
(1.9)
The average electromagnetic torque and power per electric period is nonzero only if the two mmfs are at standstill with each other. That is,
(1.10)
The positive sign (+) is used when ωr < ω1, and thus, the rotor and stator mmf waves rotate in a positive direction. The negative sign (−), used when ωr > ω1, refers to the case when the rotor mmf wave moves in the opposite direction to that of the stator. Also, the torque is nonzero when the angle γ ≠ 0, that is, when the two mmfs are phase shifted.
To produce a traveling mmf, three phases, space lagged by 120° (electrical), have to be supplied by AC currents with 120° (electrical) time-lag angles between them (see Chapter 4 in Synchronous Generators, on the SG).
So, all three phase windings for, say, maximum value of current, should independently produce a sinusoidal spatial mmf:
(1.11)
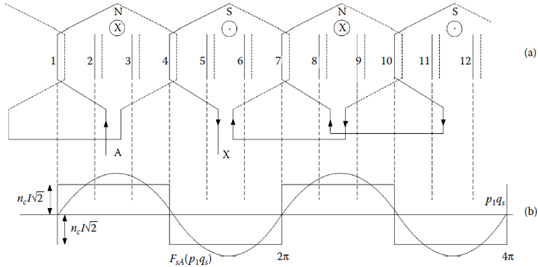
Each phase mmf has to produce 2p1 semiperiods along a mechanical period. With only one coil per pole per phase, there would be 2p1 coils per phase and 2p1 slots per phase if each coil occupies half of the slot (Figure 1.4a).
From the rectangular distribution of phase mmf (Figure 1.3a and Figure 13.b), a fundamental is extracted:
(1.12)
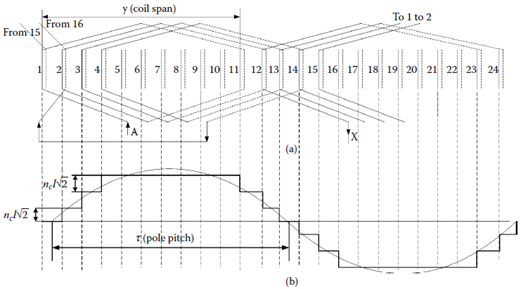
The harmonics content of the phase mmf in Figure 1.4b is hardly acceptable, but more steps in its distribution (more slots) and chorded coil would drastically reduce these space harmonics (Figure 1.5).
For the two-pole 24-slot winding with chorded coils (coil span/pole pitch = 10/12), the number of steps in the phase mmf is larger, and thus, the harmonics are reduced (Figure 1.5). For the fundamental component (based on Figure 1.5b), we obtain the expression of the mmf per pole and phase:
FIGURE 1.4 Elementary three-phase winding with 2p1 = 4 poles and Ns = 12 slots: (a) coils of phase A in series and (b) phase A magnetomotive force (mmf ) for maximum phase current.
FIGURE 1.5 Two-pole (2p1 = 2), Ns = 24 slots three-phase winding, with two layers in slot, coil span y/Ï„ = 10/12: (a) slot-to-phase allocation for layer 1 and coils of phase A and (b) phase A magnetomotive force (mmf) for maximum current.
to be continued ……….
⇒ \mu
⇒ {\mathbb R}^2]
⇒ \mid]
⇒ \approx
⇒ \widetilde{f}
⇒ \longrightarrow
⇒ \matrix{x_1&y_1&z_1@x_2&y_2&z_2@x_3&y_3&z_3}
⇒ \matrix{n\\@k}
⇒\inc{t}
FIGURE 1.2 (a) Stator and (b) rotor slotted lamination.
FIGURE 1.3 Stator and rotor stacks: (a) for axial cooling and (b) for radial-axial cooling. 
(1.8)
