In this article a 3-phase bridge type VSI with square wave pole voltages has been considered. The output from this inverter is to be fed to a 3-phase balanced load. Fig. 35.1 shows the power circuit of the three-phase inverter. This circuit may be identified as three single-phase half-bridge inverter circuits put across the same dc bus. The individual pole voltages of the 3-phase bridge circuit are identical to the square pole voltages output by single-phase half bridge or full bridge circuits. The three pole voltages of the 3-phase square wave inverter are shifted in time by one third of the output time period. These pole voltages along with some other relevant waveforms have been plotted in Fig. 35.2. The horizontal axis of the waveforms in Fig. 35.2 has been represented in terms of ‘ωt’, where ‘ω’ is the angular frequency (in radians per second) of the fundamental component of square pole voltage and ‘t’ stands for time in second. In Fig. 35.2 the phase sequence of the pole voltages is taken as V_AO, V_BO and V_CO. The numbering of the switches in Fig. 35.1 has some special significance vis-à-vis the output phase sequence.

Fig. 35.1: A 3-phase Voltage Source Inverter (VSI) feeding a balanced load

Fig. 35.2: Some relevant voltage waveforms output by a 3-phase square wave VSI

To appreciate the particular manner in which the switches have been numbered, the conduction pattern of the switches marked in Fig. 35.2 may be noted. It may be seen that with the chosen numbering the switches turn on in the sequence:- Sw1, Sw2, Sw3, Sw4, Sw5, Sw6, Sw1, Sw2, ….and so on. Identifying the switching cycle time as 360 degrees (2π radians), it can be seen that each switch conducts for 1800 and the turning on of the adjacent switch is staggered by 60 degrees. The upper and lower switches of each pole (leg) of the inverter conduct in a complementary manner. To reverse the output phase sequence, the switching sequence may simply be reversed.

Considering the symmetry in the switch conduction pattern, it may be found that at any time three switches conduct. It could be two from the upper group of switches, which are connected to positive dc bus, and one from lower group or vice-versa (i.e., one from upper group and two from lower group). According to the conduction pattern indicated in Fig. 35.2 there are six combinations of conducting switches during an output cycle:- (Sw5, Sw6, Sw1), (Sw6, Sw1, Sw2), (Sw1, Sw2, Sw3), (Sw2, Sw3, Sw4), (Sw3, Sw4, Sw5), (Sw4, Sw5, Sw6). Each of these combinations of switches conducts for 600 in the sequence mentioned above to produce output phase sequence of A, B, C. As will be shown later the fundamental component of the three output line-voltages will be balanced. The load side phase voltage waveforms turn out to be somewhat different from the pole voltage waveforms and have been dealt with in the next section.

Determination Of Load Phase-Voltages

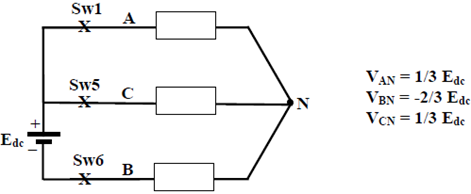
Fig. 35.1 shows a star connected balanced 3-phase load. The three load terminals are connected to the three output points (A, B, C) of the inverter. The neutral point ‘N’ of the load is deliberately left open for some good reasons mentioned later. The load side phase voltages VAN, VBN and VCN can be determined from the conduction pattern of the inverter switches. With reference to Fig. 35.2, it may be seen that for 0≤ωt≤π/3, switches Sw5, Sw6 and Sw1 conduct. Under the assumption of ideal switches Fig. 35.3(a) will represent the equivalent inverter and load circuit during the time interval 0≤ωt≤π/3. In the equivalent circuit representation the no conducting switches have been omitted and a cross (X) sign is used to represent a conducting switch. For a balanced 3-phase load the instantaneous phase voltage waveforms have been derived below for the following two cases (i) when the 3-phase load is purely resistive and (ii) when the load, in each phase, consists of a resistor in series with an inductor and a back e.m.f. In both the cases the equivalent circuit of Fig. 35.3(a) has been referred to derive the expression for load-phase voltage.

Fig. 35.3(a): Schematic load circuit during conduction of Sw5, Sw6 and Sw1

For case (i), when the load is a balance resistive load, it is very easy to see that the instantaneous phase voltages, for 0≤ωt≤π/3, will be given by V_AN= 1/3 E_dc, V_BN= -2/3 E_dc, V_CN= 1/3 E_dc.

For case (ii), the following circuit relations hold good.

${V_{AN}} = R{i_A} + L\frac{{d{i_A}}}{{dt}} + {E_A},{\rm{ }}{V_{BN}} = R{i_B} + L\frac{{d{i_B}}}{{dt}} + {E_B},{\rm{ }}{V_{CN}} = R{i_C} + L\frac{{d{i_C}}}{{dt}} + {E_C}$ . . .(35.1)

${V_{AN}} - {V_{BN}} = {E_{dc}},{\rm{ }}{V_{AN}} = {V_{CN}}$ . . . (35.2)

where i_A, i_B, i_Care the instantaneous load-phase currents entering phases A, B and C respectively. E_A, E_B, E_Cand are the instantaneous magnitudes of load phase-emfs. R and L are the per-phase load resistance and inductance that are connected in series with the corresponding phase-emf. Since the load is balanced (with its neutral point floating) the algebraic sum of the instantaneous phase currents and the phase emfs will be zero. Accordingly,

${i_A} + {i_B} + {i_C} = 0{\rm{ and }}{E_A} + {E_B} + {E_C} = 0$ . . . . . . . . (35.3)

From Eqns. 35.1 and 35.3, the following may be deduced:

${V_{AN}} + {V_{CN}} = R({i_A} + {i_C}) + L\frac{{d({i_A} + {i_C})}}{{dt}} + ({E_A} + {E_C}) = - (R{i_B} + L\frac{{d{i_B}}}{{dt}} + {E_B}) = - {V_{BN}}$ . . . . . (35.4)

Now from Eqns. 35.2 and 35.4 it can be easily found that V_AN= 1/3 E_dc, V_BN = -2/3 E_dc, V_CN = 1/3 E_dc.

Thus the instantaneous magnitudes of load phase voltages, in case of a more general (but balanced) R-L-E load are same as in case of a simple balanced resistive load.

Fig. 35.3(b) shows the equivalent circuit during π/3≤ωt≤2π/3, when the switches Sw6, Sw1 and Sw2 conduct. The instantaneous load phase voltages may be found to be V_AN= 2/3 E_dc, V_BN= V_CN= -1/3 E_dc.

Fig. 35.3(b): Schematic load circuit during conduction of Sw6, Sw1 and Sw2

The load phase voltage waveforms for other switching combinations may be found in a similar manner. Two of the phase voltages, V_AN and V _BN, along with line voltage V_AB have been plotted over two output cycles in Fig. 35.2. It may be seen that voltage V_BN is similar to V_AN but lags it by one third of the output cycle period. Further, it can be verified that the load phase voltage V_CN also has a waveform identical to the two other phase voltages but time displaced by one third of the output time period. V_CN waveform leads V_AN by 120 degrees in the time (ωt) frame. It should be obvious that the fundamental component of the phase voltage waveforms will constitute a balanced 3-phase voltage having a phase sequence A, B, C. It may also be recalled that by suitably changing the switching sequence the output phase sequence can be changed. The phase voltage waveforms of Fig. 35.2 show six steps per output cycle and are also referred as the six-stepped waveform. A more detailed analysis of the load voltage waveforms is done in the following section.

Harmonic Analysis Of Load Voltage Waveforms

The individual pole voltage waveforms output by the 3-phase square wave inverter are identical to the output waveform of a single-phase half bridge inverter. As a consequence, the harmonic analysis of the voltage waveform presented in section 34.1 of Lesson 34 is valid here too. The expression for line voltage V_AB is identical to the one given in Lesson 34 (Eqn.34.15), with ‘Φ’ of Eqn. 34.15 replaced by 2π/3 radians. For convenience the expressions for pole-A voltage ‘V_AO’ and line voltage ‘V_AB’ are shown in Fig.35.2.

${V_{AO}} = \sum\limits_{n = 1,3,5,7,...,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\sin (nwt)}$ . . . . . . . . . . . . . . . . . (35.5)

${V_{AB}} = \sum\limits_{n = 1,3,5,7,...,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\left[ {\sin nwt - \sin n(wt - \frac{{2\pi }}{3})} \right]}$ . . . . (35.6)

Using equations 35.5 and 35.6, the expressions for remaining pole and line voltages can be written simply by shifting the time (ωt) origin by the phase shift angle shown in Fig.35.2. Accordingly the expressions for pole voltage V_BOand line voltage V_BC are written below in Eqns. 35.7 and 35.8 respectively.

${V_{BO}} = \sum\limits_{n = 1,3,5,7,...,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\sin n(wt - \frac{{2\pi }}{3})}$ . . . . . . . . . . . . . . . . . . . . . (35.7)

${V_{BC}} = \sum\limits_{n = 1,3,5,7,...,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\left[ {\sin n(wt - \frac{{2\pi }}{3}) - \sin n(wt - \frac{{4\pi }}{3})} \right]}$ . . . . . . (35.8)

It may be verified that difference of V_AO and V_BO leads to the expression for V_AB. The expression for a particular harmonic component in the voltage waveforms is determined simply by substituting ‘n’ in above equations by the harmonic order. Accordingly the fundamental magnitude of line voltages V_AB, V_BC and V_CA can be written as:

${V_{AB,1}} = \frac{{2{E_{dc}}}}{\pi }\left[ {\sin wt - \sin (wt - \frac{{2\pi }}{3})} \right] = \frac{{2\sqrt 3 {E_{dc}}}}{\pi }\sin (wt + \frac{\pi }{6})$

${V_{BC,1}} = \frac{{2\sqrt 3 {E_{dc}}}}{\pi }\sin (wt - \frac{\pi }{2}),{V_{CA,1}} = \frac{{2\sqrt 3 {E_{dc}}}}{\pi }\sin (wt - \frac{{7\pi }}{6})$

The three fundamental line voltages are balanced (have identical magnitudes and are phase apart by 1200). For most practical loads only the fundamental component of the inverter output voltage is of interest. However the inverter output also contains significant amount of higher order harmonic voltages that cause undesirable distortion of the output waveform. It may, though, be noted that there are no even harmonics and the line voltages are free from 3rd and multiples of 3rd order harmonics. Also, as the harmonic order (n) increases their magnitudes decrease inversely with the harmonic order. When expressed as a fraction of fundamental voltage magnitude, the line voltage distortions are mainly due to 20% of 5th harmonic, nearly 14% of 7th, nearly 9% of 11th and nearly 8% of 13th harmonic. Since most loads are inductive in nature with a low pass filter type characteristics the effect of very high order harmonics may be neglected.

It may be noted that though the pole voltages have 3rd and multiples of 3rd order harmonic distortions, the line voltages are free from these distortions. Hence the load neutral point, rather than being connected to the mid-potential point of the input dc supply (as in a single-phase half bridge inverter), is deliberately left floating. The floating neutral point does not allow a closed path for the 3rd and multiples of 3rd harmonic currents to flow (3rd or multiples of 3rd harmonic current, if present in the load phases, have identical instantaneous magnitudes in all the three phases and their algebraic sum needs to flow in or out of the load neutral point). By keeping the load neutral point floating, not only the need for bringing out the mid-potential point of dc supply is done away with, the triplen harmonic distortions of the load current is totally eliminated. Since there are no triplen harmonic currents in the load, the load-phase voltages are also free from triplen harmonic distortions. In fact the six-stepped load-phase voltages shown in Fig. 35.2 are found to be free from triplen harmonics. It turns out that by removing all triplen harmonics from the square-shaped pole voltage waveform one can arrive at the corresponding load-phase (six-stepped) voltage waveform. Accordingly the load-phase voltages may be expressed in terms of its harmonic contents as shown below.

${V_{AN}} = \sum\limits_{n = 1,5,7,11,13....,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\sin (nwt)}$ . . . . . . . . . . . . . . . (35.9)

${V_{BN}} = \sum\limits_{n = 1,5,7,11,13....,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\sin n(wt - \frac{{2\pi }}{3})}$ . . . . . . . . . . . (35.10)

${V_{CN}} = \sum\limits_{n = 1,5,7,11,13....,\infty } {\frac{{2{E_{dc}}}}{{n\pi }}\sin n(wt + \frac{{2\pi }}{3})}$ . . . . . . . . . . . (35.11)

For a balanced three-phase load, the instantaneous magnitude of any phase current can be determined by superposition of different harmonic currents of the phase. For a simple three-phase R-L load, the phase-A current (i_A) expression in terms of resistance (R) and inductance (L) of the load may be written as:

${i_A} = \sum\limits_{n = 1,5,7,11,13....,\infty } {\frac{{2{E_{dc}}}}{{n\pi \sqrt {{R^2} + {n^2}{\omega ^2}{L^2}} }}\sin [nwt - {{\tan }^{ - 1}}\theta (\frac{{n\omega L}}{R})} ]$ . . . . . . (35.12)

Phase-B and phase-C current expressions can be obtained simply by replacingtωin Eqn. 35.12 by $(\omega t - \frac{{2\pi }}{3})$ and $(\omega t + \frac{{2\pi }}{3})$ respectively. A close look at Eqn. 35.12 will reveal that for a purely inductive 3-phase load the 5th, 7th, 11th and 13th harmonic distortion in the load current (as a percentage of fundamental component of current) will respectively be 4%, 2.04%, 0.83% and 0.59%. These distortions are much less than the corresponding distortions in the load voltage waveforms. As a result the load current for highly inductive R-L load will have close to sinusoidal shape.

Voltage And Current Ratings Of Inverter Switches

As in a single-phase square-wave inverter, switches in each leg of the three-phase inverter operate in a complementary manner. When upper switch of a leg is on the lower switch will need to block the entire dc bus voltage and vice versa. Thus the switches must be rated to block the worst-case instantaneous magnitude of dc bus voltage. An extra safety margin over the worst-case dc voltage, as discussed in Lesson-34, section 34.3, is recommended. Each inverter-switch carries load-phase current during half of the current cycle. Hence the switches must be rated to withstand the peak expected magnitude of instantaneous load-phase current. For a non-unity power factor load, the diode connected in anti-parallel with the switch will conduct part of the switch current. The distribution of current between the diode and the controlled switch will depend on the load power factor at the operating frequency. In general both diode as well as the controlled switch should be rated to carry the peak load current. These diodes also need to block a peak reverse voltage equal to worst case voltage across the switches.

Use And Limitations Of 3-Phase Square Wave Inverter

The three-phase square wave inverter as described above can be used to generate balanced three-phase ac voltages of desired (fundamental) frequency. However harmonic voltages of 5th, 7th and other non-triplen odd multiples of fundamental frequency distort the output voltage. In many cases such distortions in output voltages may not be tolerable and it may also not be practical to use filter circuits to filter out the harmonic voltages in a satisfactory manner. In such situations the inverter discussed in this lesson will not be a suitable choice. Fortunately there are some other kinds of inverters, namely pulse width modulated (PWM) inverters, discussed in the next lesson, which can provide higher quality of output voltage.

The square wave inverter discussed in this lesson may still be used for many loads, notably ac motor type loads. The motor loads are inductive in nature with the inherent quality to suppress the harmonic currents in the motor. The example of a purely inductive load discussed in the previous section illustrates the effectiveness of inductive loads in blocking higher order harmonic currents. In spite of the inherent low-pass filtering property of the motor load, the load current may still contain some harmonics. These harmonic currents cause extra iron and copper losses in the motor. They also produce unwanted torque pulsations. Fortunately the torque pulsations due to harmonic currents are of high frequencies and their effect gets subdued due to the large mechanical inertia of the drive system. The motor speed hardly changes in response to these torque pulsations. However in some cases torque pulsations of particular frequencies may cause unwanted resonance in the mechanical system of the drive. A special notch filter may then be required to remove these frequencies from the inverter output voltage.

The input dc voltage to the inverter is often derived from an ac source after rectification and filtering. A simple diode bridge rectifier followed by a filter capacitor is often the most cost-effective method to get dc voltage from ac supply. In some applications, like in un-interrupted power supplies, the dc input may be coming from a bank of batteries. In both these examples, the input dc magnitude is fairly constant. With fixed input dc voltage the square-wave inverter can output only fixed magnitude of load voltage. This does not suit the requirement in many cases where the load requires a variable voltage variable frequency (VVVF) supply. In order that ac output voltage magnitude is controllable, the inverter input voltage will need to be varied using an additional dc-to-dc converter. However a better solution will be to use a PWM inverter (to be discussed in the next lesson), which can provide a VVVF output with enhanced output voltage quality.

In spite of the limitations, discussed above, the square wave inverter may be a preferred choice on account of its simplicity and low cost. The switch control circuit is very simple and the switching frequency is significantly lower than in PWM inverters. This results in low switching losses. The switch cost may also be lower as one may do away with slower switching devices and slightly lower rated switches. Another advantage over PWM inverter is its ability to output higher magnitude of fundamental voltage than the maximum that can be output from a PWM inverter (under the given dc supply condition). Listed below are two applications where a 3-phase square wave inverter could be used.

A low cost solid-state frequency changer circuit: This circuit converts the 3-phase ac (input) voltages of one frequency to 3-phase ac (output) voltages of the desired frequency. The input ac is first converted into dc and then converted back to ac of new frequency. The square wave inverter discussed in this lesson may be used for dc to ac conversion. Such a circuit may, for example, convert 3-phase ac voltages of 50 Hz to 3-phase ac voltages of 60 Hz. The input to this circuit could as well have come from a single-phase supply, in which case the single-phase ac is first converted into dc and then converted back to 3-phase ac of the desired frequency.
An uninterrupted power supply circuit: Uninterrupted power supply circuits are used to provide uninterrupted power to some critical load. Here a critical load requiring 3-phase ac supply of fixed magnitude and frequency has been considered. In case ac mains supply fails, the 3-phase load may be electronically switched, within few milliseconds, to the output of the 3-phase square wave inverter. Input dc supply of the inverter often comes from a battery bank.

2 comments:

Abegeal CoperApril 13, 2017 at 12:35 PM
Wonderful post thank you for sharing. keep posting regarding rotary phase converters.
OmprakashJuly 27, 2017 at 4:51 PM
Your blog awesome, you had shared valuable information about Harmonic distortions are one of the most common and irritating problems in industrial environment. We need to identify the source of harmonics and suppress them for a quality supply of power. Please visit Harmonic Analysis

Please wait for approval of your comment .......

Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis

3-Phase Voltage Source Inverter With Square Wave Output

2 comments:

Popular Post