Consider an NMOS device. When Vgst the transistor is off, whatever the drain voltage i.e. Ids = 0. When Vgs>Vt, the device conducts.
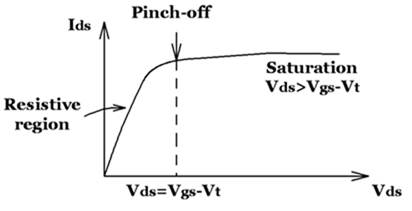
If Vgs is constant and Vds is variable then the resulting Ids Vs Vds curve have two region-
a) Resistive Region:
When Vdsgs-Vt, Vgs>Vt,
Voltage across SiO2 at source, Vgs = Vg-Vs
Voltage across SiO2 at drain, Vgd = Vg-Vd
But, voltage across SiO2 is not constant. Let’s assumed that channel is linear so voltage along the channel increases from the source to the drain. Since, the voltage across SiO2 increases from drain to source. So there are infinite capacitances.
Consider one capacitance of length dx situated at a distance x meters from the drain, as shown in figure below-
The capacitance, C = Wεdx/D
The voltage v in excess of Vt across the capacitor is,
v = Vgd + x(Vds - Vt)/L = Vgs – Vds + xVds/L - Vt
The charge, q, induced on this capacitor is,
q =Cv = Wdx (Vgs – Vds + xVds/L - Vt)/D
The total charge, Q, induced in the channel is-
Now, Q = tIds => Ids = Q/t
Where, t is time to move across the channel.
And,
t = channel length, L/electron velocity
Again,
μn = electron velocity/electric field = electron velocity/(Vds/L)
so,
Since, Vds < Vgs - Vt
so,
A linear relationship between Ids and Vds for a constant Vgs.
b) Saturation Region:
When Vds ≥ Vgs –Vt. As the drain voltage rises, the voltage across SiO2 at the drain decreases.
At Vds = Vgs - Vt
At Vds = Vgs - Vt
Vgd = Vgs – Vds = Vgs – Vgs + Vt
=>Vgd = Vt
This is the voltage necessary to just support inversion, this point on Ids Vs Vds curve is called “Pinch-off”.
At Vds>Vgs – Vt, the point at which inversion ceases moves away from the drain.
The voltage difference along the inversion channel from the source to where it ceases is Vgs – Vt and excess potential Vds – Vgs + Vt is dropped between the end of the inversion channel and the drain. It’s creates a high electric field across this very short distance and electrons are quickly swept across this area.
At and above pinch-off, the voltage between a and b is constant at Vgs – Vt. The channel length also be considered to be constant.
Thus current flow is constant and the device is said to be saturated.
So, Vds = Vgs - Vt
But, in practical situation, L decreases when Vds increases so Ids slightly increases.














0 comments:
Post a Comment
Please wait for approval of your comment .......