Three-phase full-wave Controlled Rectifier

Three-phase full-wave Controlled Rectifier with highly inductive load (Continuous load current)

Average Load/Output Voltage

${V_0} = \frac{{3\sqrt 3 {V_m}}}{\pi }\cos \alpha$

${V_0} = \frac{{3\sqrt 6 V}}{\pi }\cos \alpha$

V_m peak phase voltage

V rms phase voltage

Three-phase full-wave Controlled Rectifier with highly inductive load

Voltage and current waveforms of a three-phase full converter with a highly inductive load is shown in figure. This converter provides two quadrant operation and thyristors are fired at an interval of π/3 degrees. Since thyristors are fired every 60°, the frequency of the output ripple voltage is six times the frequency of the supply voltage. At ωt = π /6 + α, thyristor S₆ is already conducting and thyristor S₁ is turned on. For the interval ωt of π/6 to π/2 thyristors S₁ and S₆ conduct, and line to line voltage v_ab appears across the load. At ωt = π /2 + α, thyristor S₂ is turned on and thyristor S₆ is turned off due to natural commutation. This occurs because when thyristor S₂ is turned on, the line to line voltage across thyristor S₆ is the positive voltage v_bc from cathode to anode which reverse biases thyristor S₆. During the interval ωt of (π /2 + α) (5 π /6 + α), thyristors S₁ and S₂ conduct and line to line voltage appears across the load. The firing sequence of the thyristors is: 12, 23, 34, 45, 56 and 61.

The average output voltage is given by

${V_{dc}} = \frac{6}{{2\pi }}\int\limits_{\pi /6 + \alpha }^{\pi /2 + \alpha } {{V_{ab}}d\left( {\omega t} \right)}$

${V_{dc}} = \frac{3}{\pi }\int\limits_{\pi /6 + \alpha }^{\pi /2 + \alpha } {\sqrt 3 {V_m}\sin \left( {\omega t + \frac{\pi }{6}} \right)d\left( {\omega t} \right)}$

${V_{dc}} = \frac{{3\sqrt 3 {V_m}}}{\pi }\cos \alpha$

The maximum output dc voltage is given by

${V_{dm}} = \frac{{3\sqrt 3 {V_m}}}{\pi }$

The rms output voltage is given by

${V_{rms}} = {\left[ {\frac{3}{\pi }\int\limits_{\pi /6 + \alpha }^{\pi /2 + \alpha } {{{\left( {\sqrt 3 {V_m}\sin (\omega t + \frac{\pi }{6})} \right)}^2}d(\omega t)} } \right]^{\frac{1}{2}}}$

${V_{rms}} = \sqrt 3 {V_m}{\left( {\frac{1}{2} + \frac{{3\sqrt 3 }}{{4\pi }}\cos 2\alpha } \right)^{\frac{1}{2}}}$

Three-phase Converter Output Characteristics for continuous load current (Full Converter)

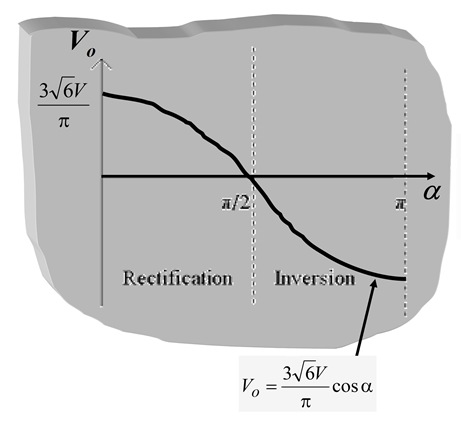
For fully controlled rectifier, The DC Motor operates in two modes.
Rectification [As Motoring]

V₀ = positive
E_a = Positive
I_o= positive
Power Flow (+ve) from input AC to DC machine

Inversion [As Regenerative Braking]

V₀ = negative
E_a = negative
I_o= positive
Power Flow (-ve) from DC machine to AC supply

Thyristor based Rectifiers (3-phase)

E_d becomes smaller as α increases, but still each thyristor conducts 120 deg. Power flow is from AC side to DC side. I_d=(E_d-E₀)/R

Thyristor based Line Commutated Inverter (3-phase)

I_d=(E_o-E_d)/R, real power flow is from DC to AC side, Polarity of E_d is reversed.
Triggering range:

Rectifier 15°-90°, inverter: 90°-165°. Thyristor may misfire for α less than 15° (def. 8°) for sudden change in line voltage and hence discontinuity in output current. If we go beyond 165°, the inverter may lose its ability to switch from one thyristor to the next. As a result currents build up very quickly until the CB trips. For safety margin max α is 150°.

previous Three-phase half-wave Controlled Rectifier

next THREE-PHASE DUAL CONVERTER

1 comment:

EbloglineeOctober 27, 2018 at 12:52 AM
More useful about AC and Dc Read here:https://www.techdoct.com/electrical/full-load-current-calculation-ac-dc-machine/?preview_id=77&preview_nonce=727269a329&post_format=standard&_thumbnail_id=1597&preview=true

Please wait for approval of your comment .......

Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis

Three-phase full-wave Controlled Rectifier

1 comment:

Popular Post