Joint modified block replacement and production/inventory control policy for a failure-prone manufacturing cell-F. Berthaut, A. Gharbi, K. Dhouib

This article considers a joint preventive maintenance (PM) and production/inventory control policy of an unreliable single machine, mono-product manufacturing cell with stochastic non-negligible corrective and preventive delays. The production/inventory control policy, which is based on the hedging point policy (HPP), consists in building and maintaining a safety stock of finished products in order to respond to demand and to avoid shortages during maintenance actions. Without considering the impact of preventive and corrective actions on the overall performance of the production system, most authors working in the reliability and maintainability domains confirm that the age-based preventive maintenance policy (ARP) outperforms the classical block-replacement policy (BRP). In order to reduce wastage incurred by the classical BRP, we consider a modified block replacement policy (MBRP), which consists in canceling a preventive maintenance action if the time elapsed since the last maintenance action exceeds a specified time threshold. The main objective of this paper is to determine the joint optimal policy that minimizes the overall cost, which is composed of corrective and preventive maintenance costs as well as inventory holding and backlog costs. A simulation model mimicking the dynamic and stochastic behavior of the manufacturing cell, based on more realistic considerations of the real behavior of industrial manufacturing cells, is proposed. Based on simulation results, the joint optimal MBRP/HPP parameters are obtained through a numerical approach that combines design of experiment, analysis of variance and response surface methodologies. The joint optimal MBRP/HPP policy is compared to classical joint ARP/HPP and BRP/HPP optimal policies, and the results show that the proposed MBRP/HPP outperforms the latter. Sensitivity analyses are also carried out in order to confirm the superiority of the proposed MBRP/HPP, and it is observed that for practitioners, the proposed joint MBRP/HPP offers not only cost savings, but is also easy to manage, as compared to the ARP/HPP policy.

1. Introduction

The bulk of industrial capital is composed of systems that produce goods and delivery services. As these systems are prone to failure with usage and age, interest in the development of efficient maintenance strategies has grown exponentially. Maintenance activities restore a system to a specified condition, and can be categorized under corrective and preventive actions. Corrective maintenance (CM) occurs at failure, while preventive maintenance (PM) occurs while a system is operating, which implies systematic inspection, detection and prevention of failures.

Barlow and Hunter introduced the concept of the age replacement PM policy (ARP), which consists of replacing a unit at failure or whenever it reaches a constant age T, and that of the block replacement PM policy (BRP), under which units are replaced at failure or at fixed intervals kT (k¼1, 2y), irrespective of the unit age. Detailed comparisons of the ARP and BRP are proposed by Barlow and Proschan, and mainly provide that the ARP is economically superior to the BRP. Although the BRP is more wasteful (i.e., almost new components are replaced when failures occur shortly before planned PM), it seems more practical to implement and to manage than the ARP since it does not require tracking unit ages and does not modify the PM planning after each maintenance operation. Several approaches have been proposed in order to improve the performance of the classical BRP: (1) Barlow and Hunter proposed the concept of minimal repair at failure (i.e., a minimally repaired system is restored to its ‘‘condition just prior to failure’’); (2) Cox and Blaming proposed the concept of inactivity (i.e., if the unit fails not long before the planned PM, it is maintained in a down state until the next PM); (3) Bhat, Tango, and Murthy and Nguyen proposed using used items (i.e., if the equipment fails not long before the PM, then the unit is replaced with a used item); and (4) Tango proposed using less reliable items (i.e., if the equipment fails not long before the PM instant, the unit is replaced with a new, less reliable item).

Berg and Epstein, as well as Archibald and Dekker, proposed a modified block replacement policy (MBRP), under which PM actions are performed at fixed intervals if the time elapsed since the last maintenance action exceeds a fixed threshold. Otherwise, the PM action is canceled, and the last installed unit is not removed, and is kept in operation. The authors showed that the MBRP strategy is better than the BRP policy, and almost as good as the ARP policy in terms of maintenance cost, when maintenance durations are negligible, while being rather simple to implement and to control in practice. For constant maintenance durations, the MBRP policy enhances the maintenance cost and the average availability of the machine as compared to the BRP policy.

In order to tackle these optimization problems, including complex renewal functions, most researchers consider that PM and CM durations are negligible with respect to the item’s lifetime. However, in most practical situations, especially for manufacturing cells, which typically operate at high utilization rates (70–80%), production interruptions due to maintenance not only affect the average system availability, but also its capacity to fulfill demand, and may result in shortage situations. In order to reduce the impact of random phenomena and shortage situations due to demand variability, process quality deterioration and machine breakdowns on the overall performance of manufacturing systems, buffer inventory has been often considered. Scheduling in this environment has also attracted many researchers, as maintenance helps improve production efficiency or product quality but it extends the make span and may cause job tardiness.

Joint consideration of production planning and corrective maintenance problems in manufacturing systems has been tackled using the optimal control theory. To control the flow rates of parts through a system subject to random failures and repairs, Kimemia and Gerschwin and Akella and Kumar introduced the hedging point policy (HPP) concept. The HPP entails the build-up and preservation of a final product safety stock while the machine is operational in order to hedge against future shortages caused by machine failures. The optimality of the HPP has been demonstrated for failure and repair times described by homogeneous Markov processes, and therefore, for a failure replacement maintenance strategy, in the case of constant demand rate and stochastic demand rate. For general failure and repair time distributions, the optimal control policy cannot be solved analytically, but the structure of the optimal inventory policy can be approximated by the HPP.

A significant branch of the literature is dedicated to minimizing the cost of combined preventive maintenance and production/inventory control policies, by considering the dynamics of a manufacturing system (buffer inventory level and machine state) and renewal approach during a maintenance cycle with constant or stochastic maintenance durations. Most of the proposed models considered failure-prone manufacturing systems composed of a single machine, and manufacturing a single product in order to respond to a constant and continuous demand. These mathematical models combined BRP or ARP with a production/inventory control policy that consists in building up and maintaining a buffer stock to respond to demand during maintenance operations. For tractability considerations, they introduced simplifying restrictive assumptions such as the one that there are no breakdowns on the machine during the build-up and depletion phases of the buffer stock. Moreover, they assumed that in shortage situations, unfulfilled demand is simply considered as lost sales, and is not backlogged at all. These assumptions are used to simplify the complex mathematical models by making the inventory level periodic with the maintenance cycle. However, the probability of a machine failing during its early life cannot be neglected, because failures during build-up periods may result in shortage situations and in high penalty costs. Based on simulation results, Rezg et al. showed that this assumption leads to different control parameters and to a 5% difference between incurred costs. In more recent works, Gharbi et al. and Rezg et al. relaxed this assumption. However, they considered that in surplus situations, the maintained machine remains non-operational until the complete depletion of the safety stock. In practical situations, breakdowns may occur during the build-up of buffer stock, and the inventory level at the end of a maintenance cycle is not necessarily periodic with stochastic maintenance durations. Chelbi and Ait-Kadi also noted that the expression of the maintenance and inventory cost involves the sum of random variables (i.e., time between failures plus CM duration), which are hard to compute for most probability distributions. Furthermore, all the papers dealing with joint preventive maintenance and production/inventory control policies only considered classical ARP or BRP. Although the MBRP represents an attractive trade-off between the BRP and the ARP, it has, to our knowledge, never been considered for non-negligible and stochastic maintenance durations, or with inventory control policies.

This article propose a joint preventive maintenance and production/inventory control policy based on MBRP and hedging point policies (HPP) for a mono-product, single-machine manufacturing cell. This relaxes the aforementioned assumptions and considers that: (1) breakdowns are allowed during build-up phases of the finished goods inventory; (2) the inventory level is not necessarily periodic with the maintenance cycle; (3) maintenance actions have non-negligible delays; and (4) unmet demand due to shortage situations is backlogged, instead of being lost. A simulation model is proposed to mimic the real dynamic and stochastic behavior of the manufacturing cell under the joint MBRP/HPP policy. The main objective of this is to compare the long-run average maintenance and inventory total cost of MBRP, ARP and BRP when combined with HPP, in order to determine the best joint preventive maintenance and production/inventory control policy. The joint optimal MBRP/HPP, ARP/HPP and BRP/HPP policies are each obtained through design of experiments, simulation analysis, and response surface methodology. This flexible resolution approach allows the exploration of the effects of a wide range of cost and time parameters on the control policies.

The rest is organized as follows: Section 2 presents the system description, the assumptions, and the structure of the three proposed control policies. The resolution approach based on simulation modeling, design of experiments, analysis of variance, and response surface methodology is presented in Section 3. Section 4 validates the proposed resolution approach and then exposes the optimal solution for a specific basic case. Section 5 provides a sensitivity analysis of the total cost with respect to corrective, preventive, inventory holding, and shortage costs. Section 6 specifically investigates the impact of the maximum production rate, the shortage cost and the CM parameters on the behavior of the optimal policy. Finally, Section 7 concludes and summarizes the main results.

2. Problem statement

2.1. System description, assumptions, and notations

The manufacturing system considered in this study is a production cell including one machine and manufacturing a single product type. The manufacturing cell can produce at a maximum capacity u_max so as to satisfy a constant finished good demand rate d, with u_max > d. The cell is prone to failure, characterized by the random variable T_f with a general probability distribution. The manufacturing machine is repaired at failure during a random amount of time T_cm and is preventively maintained during a random amount of time T_pm, where T_cm and T_pm are random variables having general probability distributions. From a practical point of view, the density probability functions of these stochastic events could be obtained from historical failure and maintenance data. CM and PM activities are characterized by their respective costs, denoted c_cm and c_pm, and their respective mean times, denoted MTCM and MTPM. At failure or at planned PM action, the manufacturing cell is with-drawn until the completion of the maintenance activity. Hence, the demand for finished goods is only met by safety stock and all unmet demands are backlogged. Inventory holding and backlog are characterized by their respective costs by time unit, denoted c⁺ and c^-. Once the production resumes, the manufacturing cell is able to satisfy backlogged demand without interrupting the normal process. As depicted in Fig. 1, the objective is to find the production rate and the preventive maintenance strategy that minimize the average total maintenance and inventory cost per unit of time.

The model under consideration includes the following commonly admitted assumptions:

1. failures are instantaneously detected;
2. the failure rate increases in time, and consequently, the likelihood of machine breakdown is reduced by PM;
3. PM and CM actions differ in terms of cost and duration (c_pm < c_cm; MTCM > MTPM);
4. breakdowns do not affect the quality of finished goods;
5. all necessary resources are available when needed; and
6. PM and CM actions restore the manufacturing cell to the as good as new operational state.

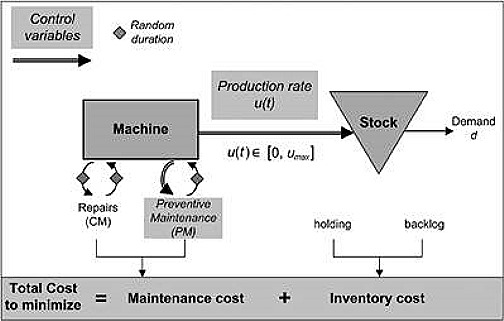
Fig. 1. Manufacturing system considered.

2.2. Formulation of the control policy

The manufacturing cell production process is controlled over time by a buffer stock control policy derived from the well-known hedging point policy, as presented below:

                               (1)

where S is the buffer stock capacity, also called the hedging point in the sphere of optimal control, x(t) is the stock level at a specified instant t, and u(t) is the manufacturing cell production rate for a specified stock level x(t). This policy entails the build-up of the buffer stock with an excess production capacity (u=u_max), which shall then be maintained at its maximum level S (u=d) in order to palliate for interruptions due to breakdowns or PM actions (u=0). Kimemia and Gerschwin and Akella and Kumar showed that the HPP is optimal for systems prone to failures described by homogeneous Markov processes (i.e., time-invariant up and down transition rates), and thus only subjected to CM. In the case of time-dependent transition rates, and especially for increasing failure rates, the dynamic programming equations that characterize the optimal control policy cannot be solved analytically, but the structure of the optimal inventory policy can be approximated by the HPP.

The manufacturing cell machine is also subjected to an MBRP policy. This article aims to analyze and compare the performance of the MBRP with classical BRP and ARP when integrated with an HPP, in order to determine the best joint policy. It should be recalled that the ARP preventively maintains the manufacturing cell machine when it reaches a given age threshold denoted T_A. The BRP consists in scheduling PM actions at regular intervals denoted T_B. The MBRP entails that PM are scheduled at regular intervals denoted T_MB1, and performed if the time elapsed since the last maintenance action exceeds a given time threshold, denoted T_MB2. Consequently, we consider the following control policies:

1. ARP/HPP, defined as a combination of ARP and HPP policies and characterized by control parameters (S, T_A);
2. BRP/HPP, defined as a combination of BRP and HPP policies and characterized by control parameters (S, T_B);
   
3. MBRP/HPP, defined as a combination of MBRP and HPP policies and characterized by control parameters (S, T_MB1, T_MB2).
   

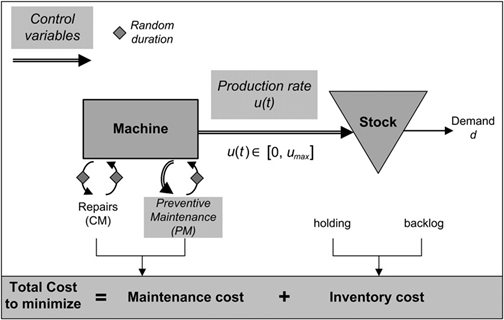
Fig. 1. Manufacturing system considered.

To our knowledge, a cost comparison of the ARP/HPP and BRP/HPP has never been tackled in the literature. Indeed, computations of the exact maintenance and inventory total cost during a maintenance cycle with the ARP or the BRP differ, and they are hard to obtain without simplifying assumptions. In fact, all proposed analytical approaches are limited to the analysis of only one maintenance cycle based on the renewal theory, and the main simplifying assumptions used are: (1) no breakdowns are allowed during the build-up of the finished goods inventory and (2) unmet demand during maintenance interventions is lost, such that the inventory periodically reaches the same level (i.e., the buffer level) after CM or PM.

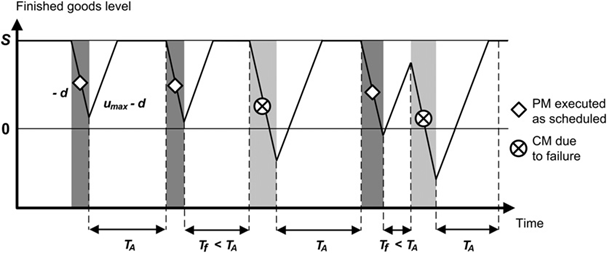
According to the effective dynamic and stochastic behavior of the manufacturing cell, we propose to relax these restrictive assumptions. Figs. 2–4 illustrate some possible scenarios of the manufacturing cell real dynamics according to the inventory level evolution under the ARP/HPP, the BRP/HPP, and the MBRP/HPP, respectively. Fig. 2 highlights that the maintenance cycle begins when production resumes after a maintenance action (CM or PM), and lasts until the next failure (if T_f < T_A), or until the next PM, if the machine does not fail before the age threshold (T_f > T_A). During maintenance periods, the inventory level decreases with a rate equal to (-d) and possibly drops below 0 (in case of shortage), which results in penalty costs. Once operational, the inventory level increases at rate (u_max-d). If the manufacturing cell machine does not fail or if its age is below T_A during the build-up phase of the safety stock, then the inventory level can reach the hedging point S, and is maintained until the occurrence of the next maintenance event (CM or PM). Note that failures or PM actions may occur during the build-up phases, and that the evolution of the inventory level is not periodic as is the case in the majority of the proposed analytical models.

Figs. 3 and 4 show the evolution of the dynamics of the inventory level under the joint BRP/HPP and MBRP/HPP policies during several maintenance cycles [kT, (k+1)T], where T denotes T_B and T_MB1 for the BRP/HPP and the MBRP/HPP, respectively. The following scenarios can be observed during the production/ maintenance process:

1. Interval [T, 2T]: The maintenance cycle begins with a PM activity during which the inventory level decreases at a rate equal to (-d). At the end of the PM operation, the system becomes operational, and the inventory level increases at rate (u_max-d) and is then maintained at level S.
2. Interval [2T, 3T]: If no failure occurs, the manufacturing cell process is shut down and a PM activity is performed at the beginning of the maintenance cycle. A failure then occurs and triggers a corrective intervention, which is completed before the end of the cycle. Production resumes shortly before the next PM action scheduled at instant 3T. The repaired machine then survives until the next scheduled PM action.
3. Interval [3T, 4T]:
   
   • Under the BRP/HPP (Fig. 3), a PM action is performed as scheduled, which triggers a fall in the inventory level to a negative value and the replacement of a relatively new component. The manufacturing cell becomes operational and does not fail until the next PM scheduled at instant 4T, allowing the inventory level to increase and to reach level S.
   • Under the MBRP/HPP (Fig. 4), the PM activity is simply skipped and the inventory level rises faster, up to its maximum level S, since a repaired machine has resumed production during interval [3T-T_MB2, 3T] and survived until 3T. It can be noted that the MBRP/HPP is less wasteful than the BRP/HPP; in fact the MBRP/HPP will generate fewer PM actions, and thus fewer new operational equipments that will be removed and rejected, and consequently, less inventory shortages.
4. Interval [4T, 5T]: Both the BRP/HPP and MBRP/HPP have the same dynamic behavior, since no repaired machine resumes production during interval [5T-T_MB2, 5T]. Several breakdowns occur in fairly quick succession during [4T, 5T], such that the threshold level is never reached. The last failure occurs before instant 5T and repairs end after the scheduled PM activity. In this case, the scheduled PM activity is skipped for both the BRP/HPP and the MBRP/HPP.

The maintenance cycles with both the BRP/HPP and the MBRP/HPP begin with a PM intervention (if not skipped), and have a constant duration T_B and T_MB1, respectively, during which the system can fail several times. Once again, the inventory level is not periodic unless restrictive assumptions are used.

In the case of negligible PM and CM durations, and irrespective of any production/inventory control policy, Archibald and Dek-ker explained that the BRP is more wasteful and less cost-effective than the MBRP and the ARP. Where we have non-negligible PM and CM durations, and when combined with an inventory control policy, the BRP/HPP should lead to consecutive inactivity periods during which the inventory can be low and can result in finished goods shortage costs, as well as in the wastage of components. Consequently, we expect the MBRP/HPP and ARP/HPP to be better than the BRP/HPP. Furthermore, since PM strategies aim to avoid most, but not all failures, the inherent problem of balancing PM and CM actions, when combined with production/inventory control, will depend not only on maintenance costs (c_pm < c_cm), but also on maintenance durations (MTCM>MTPM) and possibly on inventory shortage (). In this context, and as will be shown in the next sections, the extension of the MBRP and ARP to the MBRP/HPP and ARP/HPP would lead to conclusions that differ from those obtained by Archibald and Dekker.

Fig. 2. Evolution of the dynamics of the system under the ARP/HPP.

Fig. 3. Evolution of the dynamics of the system under the BRP/HPP.

Fig. 4. Evolution of the dynamics of the system under the MBRP/HPP.

3. Resolution approach

Beyond the restrictive assumptions proposed in the aforementioned papers, the expression of the total cost with the BRP/HPP involves nth convolution products to model the sum of random variables (i.e., the time between failures plus the CM duration), which are difficult to estimate for most probability distributions. In addition, modeling the maintenance cycle under the BRP/HPP is more complex than under the ARP/HPP (see Figs. 2 and 3). Indeed, a maintenance cycle with the BRP/HPP can include several failures between two scheduled PM activities. In this context, simple assumptions, such as no breakdowns during the inventory build-up periods, have been used both to make the inventory level periodic with the maintenance cycle and to simplify the expression of the total cost for possible scenarios based on the renewal theory (no failure or many failures between two PM activities). If skipping PM activities is allowed, as in the case of the MBRP, the number of scenarios will soar (‘‘zero or more failures between two PM’’ multiplied by ‘‘zero or more skipped PM’’), and the problem will become even more intractable.

Due to the high complexity of the problem, the joint preventive maintenance and inventory control will be tackled using simulation modeling, since it does not require the inventory trajectory to be periodic or any other restrictive assumptions. As well, simulation modeling allows any probability distribution to be used, and skipping PM can be easily considered. Simulation modeling presents two advantages: (1) the performance of the proposed policies can be obtained and compared, given that a different simulation model is developed for each joint control policy, and (2) the robustness and the flexibility of the simulation approach allows an analysis of these policies in a wide range of cost and time configurations (see Sections 5 and 6).

The resolution of the joint preventive maintenance and inventory control problem proposed in this paper required the determination of the optimum values of the control parameters (S, T_A), (S, T_B) and (S, T_MB1, T_MB2) for the ARP/HPP, BRP/HPP and MBRP/HPP, respectively. This section presents the resolution approach based on simulation modeling, design of experiments, analysis of variance and response surface methodologies. The resolution approach consists in estimating the relationship between total cost and the control parameters, based on data collected by simulation, and then in finding the location of the minimum cost for each control policy.

Fig. 5. Simulation block diagram.

3.1. Simulation model

A simulation model that combines discrete and continuous changes was developed for each of the three policies using the Visual SLAM language. The model is composed of networks and routines, which describe a specific task in the system, and is shown in Fig. 5, with the following descriptions of the different blocks:

1. The INITIALIZATION block initializes the values of the control parameters (i.e., (S, T_A), (S, T_B) or (S, T_MB1, T_MB2)) for which the simulation run is conducted as well as the values of the parameters of the system (the demand rate, the maximum production rate, the probability distributions of the lifetimes and of the maintenance durations, etc.).
2. The FAILURE block generates the lifetime, T_F, the CM and PM durations, (T_cm and T_pm, respectively), according to their probability distributions.
3. The CONTROL POLICY block provides the production rate according to Eq. (1) and the maintenance decision, as described in Figs. 2–4. A FLAG is raised whenever the inventory level crosses the threshold S or whenever the time since the last maintenance action exceeds T_MB2.
4. The STATE EQUATIONS are expressed by a C language insert and networks. They describe the inventory level and the machine age as functions of the production rate, the demand rate and the machine state (failure, CM or PM).
5. The TIME ADVANCE block changes the current time according to a time step, based on discrete event scheduling (break-down and maintenance times), continuous variable threshold crossing events and time step specifications.
6. The UPDATE inventory level and cumulative variables block traces the real-time variations of the inventory level for the chosen time step. The cumulative variables are integrated using the Runge–Kutta–Fehlberg method, as described in Pritsker and O’Reilly.
7. The UPDATE INCURRED COST block calculates the average total cost, which consists of the inventory/backlog, corrective and preventive maintenance costs.

The simulation runs until the simulation time T_sim reaches the stopping time T_end defined as the time needed to reach the steady-state.

3.2. Design of experiments, ANOVA and response surface methodology

For each joint preventive maintenance and production/inventory control policy, two (for the ARP/HPP and BRP/HPP) or three (for the MBRP/HPP) independent variables and one dependent variable (the incurred cost) are considered. We define a new variable , such that and , to make sure that The design of experiments defines how the control factors can be varied to determine the effects of the main factors and their interactions on the incurred cost with a minimal set of simulation experiments. Due to the convexity property of the cost function, complete 3² (for the ARP/HPP and BRP/HPP policies) and 3³ (for the MBRP/HPP policy) designs of experiments are carried out. A second-order regression model is proposed to estimate the cost as a function of the control parameters. Four replications were conducted for each combination, and thus 36 (3² × 4) simulation runs were made for the ARP/HPP and BRP/HPP and 108 (3³ × 4) for the MBRP/HPP.

denote the optimal PM control parameters and the optimal costs obtained through the simulation approach and analytically (I = A, B, and MB1 for the ARP/HPP, BRP/HPP, and MBRP/HPP, respectively).

The first step in the statistical analysis of the simulation results involves a multifactor analysis of variance (ANOVA), accomplished using a statistical software application (STATISTICA). The ANOVA analysis quantifies the effects of the main factors, their quadratic effects and their interactions on the dependent variable. Non-significant factors are eliminated with a level of significance (i.e., p-value>0.05). This analysis also provides the proportion of the observed variability explained by the model, which is denoted by the adjusted coefficient of determination of the model.

As a second step, the response surface methodology (RSM) is applied to estimate the relationship between the incurred cost and the input factors. For each of the three proposed policies, we assume that there exists a continuous function C of the input factors, called response surface, which gives the value of the incurred cost for any combination of these factors. Let us consider the following second-order models with standardized factors corresponding to the ARP/HPP, BRP/HPP and MBRP/HPP policies, respectively

                (2)

               (3)

                                                                                             (4)
where (α₀, α_i, α_ij,), (β₀, β_i, β_ij), (ᵞ₀, ᵞ_i, ᵞ_ij), (i, j) ∈{1,2,3} are unknown parameters and ε is the residual error. Non-significant effects are ignored or added to the residual error ε.

Using STATISTICA, the unknown parameters are estimated from the collected data. The homogeneity of the variances and the residual normality condition are also verified. The corresponding response surfaces are then computed to illustrate the location of the optimal control parameters for each joint policy.

4. Numerical application of the resolution approach

To confirm the validity of the resolution approach, the results obtained with simulation models are compared to numerical examples proposed in the literature. The resolution approach presented above is then applied to a basic illustrative example.

Table 3: Data parameters of the basic case.

umax (units/day)	d (units/day)	ccm ($)	cpm ($)	c+ ($/unit/day)	c– ($/unit/day)	Tf (days)	Tcm (days)	Tpm (days)
500	400	3000	500	1	20	Weibull (2, 20)	Log-N (1, 0.5)	Log-N (0.5, 0.1)

Table 4: ANOVA table for the MBRP/HPP.

	SS	Df	MS	F	P
TMB1	272.3486	1	272.3486	30.27403	0.000000
T2MB1	2178.873	1	2178.873	242.2015	0.000000
S	89,656.02	1	89,656.02	9966.081	0.000000
S2	26087.38	1	26,087.38	2899.850	0.000000
τ	868.2089	1	868.2089	96.50931	0.000000
τ2	66.62345	1	66.62345	7.405802	0.007734
TMB1Z	2552.108	1	2552.108	283.6900	0.000000
TMB1τ	40.77576	1	40.77576	4.532597	0.035841
Zτ	119.7359	1	119.7359	13.30973	0.000431
Block	12.10210	3	4.034034	0.448420	0.718992
Error	854.6310	95	8.996116
Total SS	122,708.8	107			R2 (adj.)=98.793

4.1. Validation of the resolution approach

The combined maintenance and inventory policies proposed in this paper have not been addressed under the same assumptions in other papers. For that reason, the validation of the simulation is conducted with the maintenance and inventory models taken separately.

On the one hand, the maintenance part is checked by comparing the control parameters and the costs obtained with the proposed resolution approach to those obtained analytically in Archibald and Dekker [14] with the data parameters shown in Table 1. The first and second numbers of the Weibull distribution denote the shape and the scale parameters, respectively, and the results are summarized in Table 2, which highlights the fact that the cost difference between the two approaches is negligible (relative errors below 0.5%).

The inventory part of the simulation model was tested by comparing the simulation results with the analytical results of Akella and Kumar [22] for exponential failure and repair times (i.e., non-increasing failure rate). PM is not performed and the ARP, BRP, and MBRP are boiled down to the same maintenance policy (i.e., the failure replacement policy). The corresponding simulation model and the results of this comparison are similar to those presented in Kenne´ and Gharbi [28].

These tests validate the simulation modeling and the resolution approach adopted in this paper. The model is then run in order to jointly take into account maintenance and inventory policies and to solve the optimization problem for a basic case.

4.2. Detailed results for a basic case

The resolution approach and the results are detailed in a step-by-step manner for the basic case presented in Table 3. The manufacturing system considered here is designed to produce at a maximum production rate 25% higher than the demand rate. The stochastic time variables that describe the time between failures and the CM and PM durations follow Weibull and Lognormal distributions, respectively (the first and second values within parentheses indicate the mean and the standard deviation for the lognormal distribution). The maintenance parameters are such that CM takes twice as long and costs six times as much as PM. Backlogs are penalized by a cost 20 times as high as the holding cost.

To ensure that a steady-state is reached, the duration of the simulation runs is set to 1,000,000 units of time, given by preliminary runs. Simulation runs are conducted according to the designs of experiments presented in the previous section.

First, ANOVA analyses are carried out on the collected data, as presented in Table 4 for the MBRP/HPP. All the factors, interactions and quadratic effects are significant (po0.05). The R² adjusted value has a value of 98.793%, which implies that more than 98% of the total variability is explained by the model [41]. The model, which is composed of the factors, their interactions and the quadratic effects, fits the basic case data. The ANOVA tables for the ARP/HPP and BRP/HPP lead to the same conclusions, with R² adjusted values of 98.387% and 98.283%, respectively.

The corresponding cost functions are given as follows for the MBRP/HPP, the BRP/HPP and the ARP/HPP policies, respectively:

                                                           (5)

             (6)

             (7)

Fig. 6 presents the projection of the cost response surface on two-dimensional planes for the MBRP/HPP. The minimum total cost, , is located at , , and , these values being the optimal control parameters that should be applied with the MBRP/HPP. Similarly, the optimal total costs for BRP/HPP and ARP/HPP are , located at , , and , located at , , respectively.

The advantage of the simulation-based approach also lies in providing the possibility of easy collection and analyzing several performance indices. Table 5 presents complementary performance indices obtained by simulation with the previous optimal control parameters.

According to Table 5, the average lifetime and availability of the machine confirm that the best use of the machine is obtained under the ARP/HPP and the MBRP/HPP and that the BRP/HPP triggers a wastage of relatively new components. Since the MBRP/HPP skips PM interventions if the time since the last maintenance action is below T_MB2, the resulting maintenance cost is almost as good as that obtained with the ARP/HPP. The inventory policy for the BRP/HPP suffers from consecutive inactive periods caused by breakdowns that occur shortly before scheduled PM, unlike the ARP/HPP and the MBRP/HPP, whose age thresholds enable a wider spacing of maintenance actions. As a result, the optimal inventory level under the BRP/HPP requires a higher hedging point than under the ARP/HPP and the MBRP/HPP in order to avoid inventory shortage. Consequently, the joint BRP/HPP policy is the most expensive amongst the three proposed policies. When comparing the ARP/HPP and the MBRP/HPP, we observe that the MBRP/HPP triggers fewer PM actions and almost as many failures as with the ARP/HPP. Inactive periods are consequently scarcer with the MBRP/HPP than with the ARP/HPP, which explains why the optimal hedging point and inventory costs are higher with the ARP/HPP than with the MBRP/HPP.

Fig. 6. Cost response surfaces for the MBRP/HPP.

Table 5: Complementary performance indices measured by simulation.

^aX⁺ and X ^– denote the average positive and negative inventory levels, respectively.

Table 6: Comparison of the optimal maintenance control policies.

^a∆_{i, ARP} denotes the relative deviation from the maintenance cost obtained with the ARP policy.
From the preceding discussion, we can draw the following conclusions for the basic case:

1. The BRP/HPP is the least efficient policy amongst the proposed policies, in terms of both inventory and maintenance costs.
2. The MBRP/HPP is better than the ARP/HPP. In fact, the ARP/HPP slightly outperforms the MBRP/HPP in terms of maintenance cost, whereas the latter is better in terms of inventory cost.

The optimal control parameters of the maintenance control policies obtained by simulation without considering any production/inventory control policy are presented in Table 6. On the one hand, these results extend those presented by Archibald and Dekker [14] to the case of non-negligible and stochastic maintenance durations. On the other hand, a comparison between the previous results and Table 6 shows how inventory control combined with maintenance affects the optimal maintenance control parameters. The optimal values of T_i and τ in the joint control policies are, respectively, significantly lower and higher than for the maintenance strategy, when the production/inventory control is not considered. Indeed, PM in the joint control policy are more often performed and more often skipped in order to avoid failures and consecutive inactive periods, which lead to shortage situations.

Table 7: Combination of cost parameters of the sensitivity analysis.

5. General sensitivity analysis of cost parameters

Another set of experiments is considered to measure the sensitivity of the proposed control policies with respect to cost parameters. The goal is to demonstrate the efficiency, the robust-ness of the resolution approach and to study the behavior of each control policy when varying cost parameters.

Table 7 presents nine configurations of cost parameters derived from the basic case (case 1) by changing them to higher and lower values, one at a time. Table 8 highlights the consistency between the variation of each cost parameter and the optimal control parameters and costs. As observed in the previous section, we noticed that the inventory cost is larger and the maintenance cost is lower under the ARP/HPP than under the MBRP/HPP.

The first observation from Table 8 is that the optimum control parameters evolve in the same direction and with the same magnitude in response to any variation in cost parameters. Their variations are examined and compared to the basic case as follows:

1. Variation of the CM cost c_cm (cases 2 and 3): When the CM cost increases (case 3), the joint control policies give preference to PM. Thereby, the time thresholds ( and ) and the intervals between periodic PM ( and ) decrease. In this situation, the average number of failures decreases, whereas the number of PM actions increases. Consequently, the inventory controls require a slightly higher hedging point S^*. An increase in the CM costs leads both to a decrease in the inventory/backlog cost and to an increase in the maintenance cost, but the overall cost increases. A decrease in the CM cost has the opposite effects (case 2).
   Table 8: Sensitivity analysis for different cost parameters.
   
   ^a T_i denotes T_B, T_A, and T_MB1 for the BRP/HPP, ARP/HPP, and MBRP/HPP policies, respectively.
   Table 9: Cost difference confidence intervals (95%) of the ARP/HPP, BRP/HPP, and MBRP/HPP for cases 1–9.
   
2. Variation of the PM cost c_pm (cases 4 and 5): A variation of the PM cost has the opposite effect when compared with the variation of the CM cost. Indeed, they both affect the optimal balance between PM and CM.
3. Variation of the holding cost c⁺ (cases 6 and 7): When the holding cost increases (case 7), all the joint control policies react by lowering the hedging point S*. The average inventory levels will then decrease, while the risk of shortage increases. The maintenance control policies adapt to avoid breakdowns by lowering the PM intervals ( and ) and the time thresholds ( and ). The total cost increases in response to an increase in the holding cost. Note that a decrease in the holding cost has the opposite effects (case 6).
4. Variation of the shortage cost c^- (cases 8 and 9): The tolerance for risk of shortage in the system is affected by any variations of the shortage cost. To avoid shortages, PM should be performed more frequently and the inventory level should be higher when the shortage cost increases (case 9). As a result, the PM intervals ( and ) and the time thresholds ( and ) decrease, while the hedging points S^* increase. An increase in the total cost is also observed for each joint control policy. Note that a decrease in the holding cost has the opposite effects (case 8).

From the optimal costs of the ARP/HPP, BRP/HPP, and MBRP/HPP observed in Table 8, we notice that the MBRP/HPP outperforms both the BRP/HPP (at least 12.46%, and up to 17.16% better) and the ARP/HPP (at least 2.04%, and up to 3.28% better). To confirm these observations, and hence the advantages of the MBRP/HPP over the BRP/HPP and the ARP/HPP are in terms of costs, a Student’s t-test is conducted [41]. The 95% confidence interval of the difference between the costs obtained with the ARP/HPP and MBRP/HPP, , as well as those of and , are presented in Table 9. Since the lower bounds of the confidence intervals of the cost differences are positive in all cases at a 95% confidence level (, and ), we confirm that the BRP/HPP is the least efficient control policy and that the MBRP/HPP is not only easier to implement and manage but also better than the ARP/HPP in terms of total cost.

6. Influence of the maximum production rate, the shortage cost, and the CM parameters

In the last section, we observed the effects of variations of the cost parameters on the optimal control parameters and on the incurred total cost for each control policy. It showed the advantages of MBRP/HPP over the ARP/HPP and the BRP/HPP in terms of total cost. The objective of this section is to give a better insight into the feasibility of the system (i.e., its capacity to fulfill the demand), the cost differences and the availability of the system when varying the maximum production rate, the shortage cost, and the CM parameters.

6.1. Feasibility condition

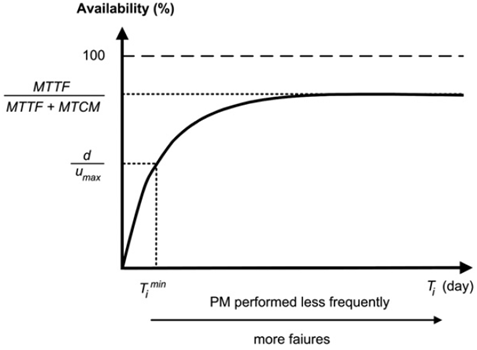
Section 4.2 showed that extending the maintenance strategies to the joint preventive maintenance and production/inventory control policies modifies the preventive maintenance parameters, causing the PM to be performed and skipped more often than in the case without inventory control in order to avoid failures and consecutive inactive periods. However, the incurred availability of the system becomes lower and approaches the feasibility condition of the system, which entails that the operational availability of the system must be larger than d/u_max so as to satisfy demand in the long run. The system availability for the proposed control policies is a function of the maintenance parameters, and does not depend on the hedging point level. Fig. 7 illustrates the relation-ship between the availability, the occurrences of failures and the feasibility condition for the previous joint control policies when varying the preventive maintenance parameter T_i, i=A, B and MB1 (with a given τ for the MBRP/HPP policy).

If T_i increases, then PM is performed less often, and the availability increases and reaches an asymptotic value, which corresponds to the manufacturing cell availability under a replacement on failure strategy (i.e., MTTF/(MTTF+MTCM)=94.66% for the basic case, where MTTF denotes the mean time to failure). On the other hand, if T_i decreases, then the availability decreases and reaches the feasibility condition, which imposes a minimal value for T_i, and thus influences the choice of the control parameters. For instance, the availability must be larger than d/u_max =80% for u_max =500 and 88.89% for u_max =450, which implies that T_A must be larger than 2.03 and 4.24, respectively. With the parameters of the basic case, if u_max <423, then the system is not feasible. However, if u_max is just over 423, then the system will be hardly feasible, the inventory build-up period will be long and there will be frequent shortages.

6.2. Influence of the maximum production rate

Fig. 8 shows, for the basic case, the relative cost difference between the MBRP/HPP and the BRP/HPP as compared with the ARP/HPP (denoted by ) when the maximum production rate u_max goes up incrementally. The manufacturing cell availability evolution as a function of u_max for the studied joint control policies is also depicted in Fig. 8. A variation of the maximum production rate affects the build-up and shortage durations. Since the BRP/HPP leads to consecutive inactive periods, the relative cost difference between the BRP/HPP and ARP/HPP increases when the maximum production rate decreases. The MBRP/HPP policy skips more and more PM in order to allow the inventory level to build up and reach its maximum level. As shown for the basic case in Table 5, the MBRP/HPP undergoes fewer shortages than the ARP/HPP, and this difference becomes more marked as u_max decreases. For this reason, the relative difference between the MBRP/HPP and the ARP/HPP increases when the maximum production rate decreases. Fig. 8 also highlights the fact that when u_max falls below 550, the total costs significantly diverge and their avail-abilities significantly increase, since the feasibility condition imposes a minimal value for the time between PM, and thus imposes the choice of the optimal control parameters. We can conclude that the MBRP/HPP behaves significantly better than the ARP/HPP and BRP/HPP when the system is close to the feasibility condition.

Fig. 7. Availability of the system according to T_i, i=A, B, MB1.

Fig. 8. Effects of the maximum production rate on the control policies.

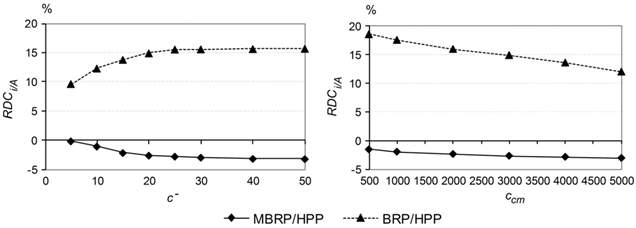
6.3. Influence of shortage cost and CM cost parameters

In this section, the shortage cost has been varied from 5 to 50 (c^- /c⁺ varies from 5 to 50) and the CM cost from 500 to 5000 (c_cm/c_pm varies from 1 to 10). All other parameters remain unchanged, with the numerical values defined in the basic case. The relative cost differences between the BRP/HPP and the MBRP/HPP as compared with the ARP/HPP and their operational availabilities are depicted in Figs. 9 and 10, respectively.

If the CM cost increases, then the optimal policies give preference to PM in order to avoid breakdowns, and the avail-ability of the system decreases for the three policies (see Fig. 10). The benefits gained from skipping PM interventions with the MBRP/HPP become more and more significant when PM is more frequently scheduled, and thus the relative cost difference between the MBRP/HPP and ARP/HPP decreases (Fig. 9). Since the number of breakdowns decreases in response to an increase in the CM cost, the number of consecutive inactive periods observed with the BRP/HPP decreases, and consequently, the cost difference between the BRP/HPP and the ARP/HPP decreases.

On the other hand, if the shortage cost increases, then the hedging point level increases to palliate for future interruptions due to CM or PM, and the maintenance policies evolve to limit long inactive periods with more frequent PM. As observed in Figs. 9 and 10, the joint control policies are more sensitive to the shortage cost than to the CM cost. The advantages of the ARP/HPP over the BRP/HPP increase when the shortage cost increases, because the main drawback of the BRP/HPP lies in the

Fig. 9. Effects of the shortage cost and of the CM cost on the total cost.

Fig. 10. Effects of the shortage cost and of the CM cost on the availability.

risk of consecutive CM and PM, and thus the risk of backlogs. As for the basic case, the MBRP/HPP leads to average positive and negative inventory levels that are slightly lower than under the ARP/HPP and to a better inventory cost. A higher value of c^- increases the difference between their inventory costs and results in a decrease in the cost difference between the MBRP/HPP and the ARP/HPP. When the shortage cost increases, the availabilities decrease and reach an asymptotic limit, which is a trade-off between the feasibility condition and the number of failures. Similarly, the cost differences tend to stabilize for high shortage cost values.

The main conclusion is that if shortages or breakdowns lead to more penalties, then the MBRP/HPP significantly outperforms the ARP/HPP.

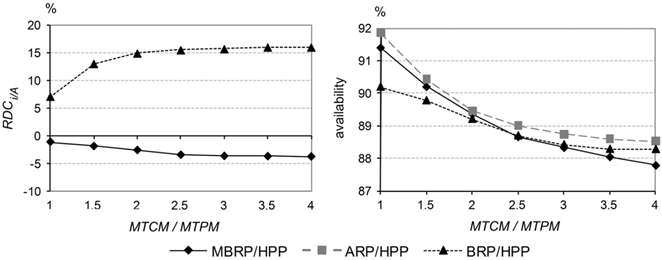
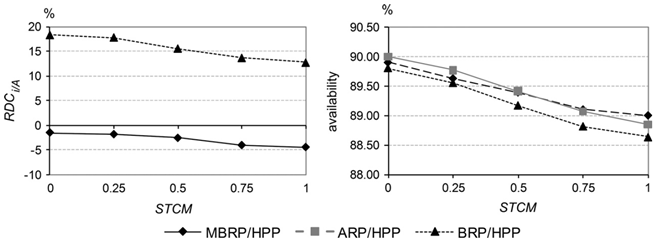
6.4. Influence of the time to execute corrective maintenance

Another set of experiments was conducted in order to analyze the effects of the mean time to corrective maintenance (MTCM) and its standard deviation (SDCM) on the joint optimal control policies. The relative cost differences between the MBRP/HPP and the BRP/HPP and the ARP/HPP and the availability of the system under each control policy are presented in Fig. 11 when varying the MTCM from 0.5 to 2 (MTCM/MTPM varies from 1 to 4), and in Fig. 12 when varying the SDCM from 0 to 1. All other parameters are the same as in the basic case.

As expected, the optimal joint control policies give more and more preference to PM in order to avoid breakdowns and shortages when the MTCM or SDCM increases. The benefits gained from skipping PM interventions with the MBRP/HPP become more and more significant when PM is more frequently scheduled, and thus the relative cost difference between the MBRP/HPP and ARP/HPP decreases. It can be seen that varying the MTCM has the same effect as does the shortage cost on total costs and on the availabilities of the joint control policies, since they both affect backlogs.

7. Concluding remarks

A joint preventive maintenance and production/inventory control policy for a single-machine, mono-product manufacturing cell has been proposed. The production inventory control policy is based on the HPP, which allows the building of a safety stock to hedge against demand shortages during shutdown periods caused by corrective and preventive activities. The preventive maintenance policy is based on the MBRP, which entails that maintenance of the manufacturing cell be performed at failures or at scheduled periods if the time since the last maintenance action is below a specified threshold age.

A general simulation model has been considered to mimic the real dynamic and stochastic behavior of the manufacturing cell. The proposed model relaxes many simplifying and unrealistic assumptions considered by several authors in many contributions such as: (1) breakdowns are not allowed during build-up of the finished goods inventory; (2) the inventory level is periodic with the maintenance cycle; (3) corrective and maintenance actions have negligible delays; and (4) unmet demands due to shortage situations are lost, instead of being backlogged. The optimal solution for the joint MBRP/HPP problem is obtained through a numerical approach that combines experimental design, simulation modeling, analysis of variance and response surface methodologies.

Fig. 11. Effects of mean time to perform CM on the total cost and on the availability.

Fig. 12. Effects of standard deviation of the time to perform CM on the total cost and on the availability.

The joint MBRP/HPP is compared to the joint BRP/HPP and the joint ARP/HPP by considering the cost incurred by preventive and corrective activities, holding inventories, and demand shortages. Without considering the impact of maintenance activities on the overall performance of the manufacturing system, most authors working in the reliability and maintainability fields mention that ARP policy outperforms the BRP policy. In spite of its wasteful character, the BRP policy is more generally considered and implemented in the industrial context since it is more practical and easy to manage than the ARP policy. By jointly considering preventive maintenance and production/inventory control policies, the results show that the proposed MBRP/HPP policy out-performs the BRP/HPP and ARP/HPP policies in terms of incurred total cost. In addition, the MBRP is as easy to implement and to manage as the BRP policy. This reinforces the interest of the MBRP when integrated with inventory control in real manufacturing context.

This article should stimulate further research on joint maintenance and production/inventory control. We considered some of the most ‘‘popular’’ or classical maintenance and production/ inventory control policies proposed in the literature or used in practice. We suggest that other maintenance strategies and other production/inventory policies should be investigated. To that purpose, the simulation-based resolution approach proposed in this paper should prevail over analytical approaches in consider-ing complex models because many restrictive assumptions can be relaxed and it also allows for an easy collection of complementary performance indices and so a more thorough analysis.