Switching transients in the general case

Under practical conditions, it is necessary to consider inductance and resistance. First consider the addition of series inductance in Figure 6.16. In any practical TSC circuit, there must always be at least enough series inductance to keep di/dt within the capability of the thyristors. In some circuits there may be more than this minimum inductance. In the following, resistance will be neglected because it is generally small and its omission makes no significant difference to the calculation of the first few peaks of voltage and current.

The presence of inductance and capacitance together makes the transients oscillatory. The natural frequency of the transients will be shown to be a key factor in the magnitudes of the voltages and currents after switching, yet it is not entirely under the designer's control because the total series inductance includes the supply-system inductance which, if known at all, may be known only approximately. It also includes the inductance of the step-down transformer (if used), which is subject to other constraints and cannot be chosen freely.

It may not always be possible to connect the capacitor at a crest value of the supply voltage. It is necessary to ask what other events in the supply-voltage cycle can be detected and used to initiate the gating of the thyristors, and what will be the resulting transients.

The circuit is that of Figure 6.17. The voltage equation in terms of the Laplace transform is

             (6.11)

Fig. 6.17 Circuit for analysis of practical capacitor switching.

The supply voltage is given by v = v̂ sin (ω₀t + α). Time is measured from the first instant when a thyristor is gated, corresponding to the angle α on the voltage wave- form. By straightforward transform manipulation and inverse transformation we get the instantaneous current expressed as

        (6.12)

where ω_n is the natural frequency of the circuit
            (6.13)

and

              (6.14)

n is the per-unit natural frequency.
The current has a fundamental-frequency component i_AC which leads the supply voltage by π/2 radians. Its amplitude î_AC is given by
             (6.15)

and is naturally proportional to the fundamental-frequency susceptance of the capacitance and inductance in series, that is, B_cn²/(n²-1). The term n²/(n²-1) is a magnification factor, which accounts for the partial series-tuning of the L-C circuit. If there is appreciable inductance, n can be as low as 2.5, or even lower, and the magnification factor can reach l .2 or higher. It is plotted in Figure 6.18.

The last two terms on the right-hand side of equation (6.12) represent the expected oscillatory components of current having the frequency ω_n. In practice, resistance causes these terms to decay. The next section considers the behavior of the oscillatory components under important practical conditions.

Fig. 6.18 Voltage and current magnification factor n²/(n² - 1).

1. Necessary condition for transient-free switching. For transient-free switching, the oscillatory components of current in equation (6.12) must be zero. This can happen only when the following two conditions are simultaneously satisfied:

             (6.16)

            (6.17)

The first of these equations means that the thyristors must be gated at a positive or negative crest of the supply voltage sinewave. The second one means that the capacitors must also be precharged to the voltage v̂n²/(n² - 1) with the same polarity. The presence of inductance means that for transient-free switching the capacitor must be 'overcharged' beyond v̂ by the magnification factor n²/(n² - 1). With low values of n, this factor can be appreciable (Figure 6.18).

Of the two conditions necessary for transient-free switching, the precharging condition expressed by equation (6.17) is strictly outside the control of the gating-control circuits because V­_C0, n, and v̂ can all vary during the period of non- conduction before the thyristors are gated. The capacitor will be slowly discharging, reducing V­_C0; while the supply system voltage and effective inductance may change in an unknown way, changing n. In general, therefore, it will be impossible to guarantee perfect transient-free reconnection.

In practice the control strategy should cause the thyristors to be gated in such a way as to keep the oscillatory transients within acceptable limits. Of the two conditions given by equations (6.16) and (6.17), the first one can in principle always be satisfied. The second one can be approximately satisfied under normal conditions. For a range of system voltages near 1 p.u., equation (6.17) will be nearly satisfied if the capacitor does not discharge (during a non-conducting period) to a very low voltage: or if it is kept precharged or 'topped up' to a voltage near ±v̂n²/(n+2 - 1).

2. Switching transients under non-ideal conditions. There are some circumstances in which equations (6.16) and (6.17) are far from being satisfied. One is when the capacitor is completely discharged, as for example when the compensator has been switched off for a while. Then V_C0 = 0. There is then no point on the voltage wave when both conditions are simultaneously satisfied.

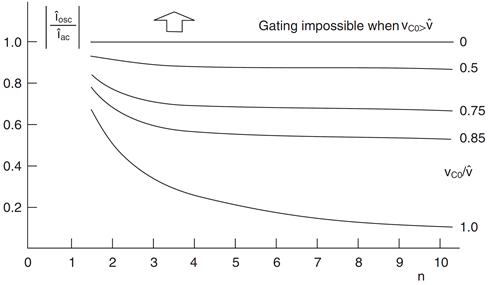
In the most general case V_C0 can have any value, depending on the conditions under which conduction last ceased and the time since it did so. The question then arises, how does the amplitude of the oscillatory component depend on V_C0? How can the gating instants be chosen to minimize the oscillatory component? Two practical choices of gating are: (a) at the instant when v = V_C0, giving sin α = V_C0/v̂; and (b) when dv/dt = 0, giving cos α = 0. The first of these may never occur if the capacitor is overcharged beyond v̂. The amplitude î_osc of the oscillatory component of current can be determined from equation (6.12) for the two alternative gating angles. In Figures 6.19 and 6.20 the resulting value of î_osc relative to î_AC is shown as a function of V_C0 and n, for each of the two gating angles.

From these two figures it is apparent that if V_C0 is exactly equal to v̂, the oscillatory component of current is non-zero and has the same amplitude for both gating angles, whatever the value of the natural frequency n. For any value of V_c0 less than v̂, gating with v = V_C0 always gives the smaller oscillatory component whatever the value of n.

Fig. 6.19 Amplitude of oscillatory current component. Thyristors gated when v = Vco.

Fig. 6.20 Amplitude of oscillatory current component. Thyristors gated when dv/dt = 0.

The conditions for transient-free switching appear in Figure 6.20 in terms of the precharge voltage required for two particular natural frequencies corresponding to n = 2.3 and n = 3.6.

Switching a discharged capacitor

In this case V_C0 = 0. The two gating angles discussed were: (a) when v = V_C0 = 0; and (b) when dv/dt = 0 ( cos α = 0). In the former case only equation (6.17) is satisfied. From equation (6.12) it can be seen that in the second case (gating when dv/dt = 0) the oscillatory component of current is greater than in the first case (gating when v = V_C0 = 0). An example is shown in Figure 6.21 and Figure 6.22.

Fig. 6.21 Switching a discharge capacitor; circuit diagram.

Fig. 6.22 Switching transients with discharge capacitor. (a) gating when V = V_C0 = 0; (b) gating when dv/dt = 0.

The reactances are chosen such at î_AC = 1 p.u. and the natural frequency is given by n = X_C((X_S + X_T) = 3.6 p.u. In case (a), the amplitude of the oscillatory component of current is exactly equal to î_AC. In case (b), the oscillatory component has the amplitude nî_AC and much higher current peaks are experienced. The capacitor experiences higher voltage peaks and the supply voltage distortion is greater.

previous Switching transients and the concept of transient-free switching

next Voltage-source converters (VSCs) and derived controllers