Wind Energy Measurements

previous Wind Turbines types and components

There are four measurements associated with wind energy, the measurements of electrical signals including voltage, current or collectively electrical power, wind turbine rotational speed and the wind speed.

Electrical measurements

In order to determine electrical energy output, it is necessary to be able to measure it either directly as energy in kWh, or indirectly by measuring the voltage, current of the generated output of the wind turbine.

Ohms Law

Ohm's law states that the current (I) through a conductor between two points is proportional to the potential difference (V) and inversely proportional to the resistance (R).

Figure 5.1 Ohms Law

Electrical Power

Electrical power (E) is the amount of energy produced.
The unit of measurement of Power being the Watt (W) with prefixes used to denote milliwatts (mW = 10^-3W) or kilowatts (kW = 10³W).

By using Ohm's law and substituting for V (volts), I (amps) and R (Ω)the formula for electrical power, E (watts) can be found as:

Alternating Current Power

As in the case with DC power, the instantaneous electric power in an AC circuit is given by

 

But these quantities are continuously varying. Almost always the desired power in an AC circuit is the average power, which is given by

Where φ is the phase angle between the current and the voltage and where V and I are understood to be the effective or rms values of the voltage and current, see Figure 5.2. The term cos φ is called the "power factor" for the circuit, a power factor of one or "unity power factor" is the goal of any electric utility company since if the power factor is less than one, they have to supply more current to the user for a given amount of power use. In so doing, they incur more line losses. They also must have larger capacity equipment in place than would be otherwise necessary.

Figure 5.2 Resistive AC circuit

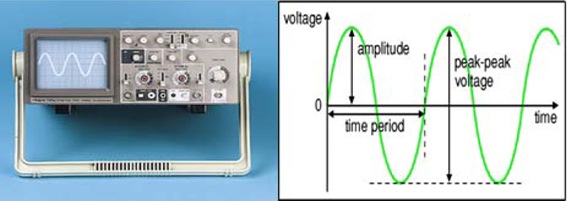
The difference between the maximum and minimum values is called peak-to-peak voltage (V_pp) and is twice the peak Voltage (V_p). The RMS voltage. (V_rms) is related to the peak voltage as:

Circuit currents and voltages in AC circuits are generally stated as root-mean-square or rms values rather than by quoting the maximum values. The root-mean-square for a current is defined by

That is, you take the square of the current and average it, then take the square root. When this process is carried out for a sinusoidal current

Since the AC voltage is also sinusoidal, the form of the rms voltage is the same. These rms values are just the effective value needed in the expression for average power:

Since the voltage and current are both sinusoidal, the power expression can be expressed in terms of the squares of sine or cosine functions, and the average of a sine or cosine squared over a whole period is = 1/2.

next Electrical Measurements