The zero-state response, the impulse response, and convolution

Here,
computing the zero-state response by convolution, practicing convolution, the delta function and how it is defined, the
impulse response of a LTI system and formula for computing it will be discussed.
The zero-state response; sums of inputs
Let us now find the response to an input f(t) when the initial conditions are set to 0; this is the zero-state response.
Important idea: Suppose we can decompose the input function f(t) into a bunch of functions:




Then, by linearity, the output of the system will be the sum of the responses due to these component functions:




If we do the decomposition of f(t) in a smart way, each of the components will be easier to compute, where y_i is the response to f_i(t).
Think of writing f(t) as a set of very narrow rectangles of width ∆τ, with amplitude f(n∆τ ) for the nth rectangle. Then f(t) is the sum of all the slices. Then we want to find the response for each slice, and add them up.
Let us introduce some notation to describe this idea. Let δ_∆τ (t) be a pulse starting at t = 0, with width ∆τ and height 1/∆τ, so that δ_∆τ (0)∆τ is equal to 1. (Note that δ_∆τ (t) has area 1 for any ∆τ) Then



and




Now, in the limit, δ_∆τ(t)→ δ(t), and we obtain




This thus describes our input function, as a sum of “simpler" functions.
Now let us describe the output function. Let h_∆τ(t) be the output response to the input δ_∆τ(t). Then, by time-invariance, h_∆τ(t- n∆τ) is the response to δ_∆τ(t- n∆τ). Then we add up the results:




Now take the limit: let h(t) be the response to δ(t). The function h(t), again, is the response of the system when a δ function is input (when all the initial conditions of the system are zero). We call it the impulse response.
Then we get




So, for an arbitrary input f(t), we can find the output using this integral. The key is that we need to know h(t), which is only a function of the system.
This integral comes up often enough (since it arises for any LTI system) that it has been given a name: This is the convolution integral. Often we denote the
operation using a*:




The * does not denote multiplication: it denotes convolution. Note location of t in the integral.
Properties of convolution:
Commutative f₁(t) * f₂(t) = f₂(t) * f₁(t). (Proof: let x = t - τ)
Distributive f₁(t) * [f₂(t) + f₃(t)] = f₁(t) * f₂(t) + f₁(t) * f₃(t). (Follows from linearity of integral.)
Associative f₁(t) * [f₂(t) * f₃(t)] = [f₁(t) * f₂(t)] * f₃(t).
Shift If f₁(t) * f₂(t) = c(t) then
f₁(t) * f₂(t - T) = c(t - T)
f₁(t - T) * f₂(t) = c(t - T)
f₁(t - T₁) * f₂(t - T₂) = c(t - T₁ - T₂)
Convolution with delta f(t) * δ (t) = f(t).
Width If f₁(t) has duration W₁ and f₂(t) has duration W₂, then f₁(t) * f₂(t) has duration W₁ +W₂.
Causal signal: f(t) = 0 for t < 0. Causal system: output cannot begin before the input begins. If f(t) is causal,




If the system is causal, then for t < 0 we must have h(t) = 0. Then




(the 0^- picks up the delta function at the origin, if any).

Example 1: f(t) = e^-tu(t) and h(t) = e^-2tu(t) (causal functions). Then




Note that there is a table (which will save a lot of work). As an example from the table,




(Observe: no exponential terms come out that were not there in the first place.)
The total response of the system is given by






The impulse response function h(t)

Given that the impulse response function is so important to the zero-state solution, how can we find it? The unit impulse response function is the response of a system with zero initial conditions to an impulse input: imagine the effect of a sledge hammer hitting the bumper of a car, or a short pulse into a circuit. The impulse response function is, to some ways of thinking, merely a mathematical artifice, but it provides us a powerful tool for finding the output of a system with an arbitrary input function. The unit impulse response function consists of the characteristic mode terms of the system, for all t ≥ 0⁺. If there is a direct connection from the input to the output (by some path), there may also be a delta function in the impulse response function at time t = 0:

h(t) = A₀δ(t) + characteristic mode terms; t ≥ 0:
For a system
Q(D)y(t) = P(D)f(t)
which may be written in expanded form as
(Dⁿ + a_n-1D^n-1 + . . . . + a₁D + a₀)y(t) = (b_nDⁿ + b_n-1D^n-1 + . . . . + b₁D + b₀)f(t)
the unit impulse response function for the system may be found as follows:
1. Find the zero-input response y₀(t),
                                             Q(D)y₀(t) = 0
    subject to the initial conditions




2. Then
h(t) = b_nδ(t) + [P(D)y₀(t)]u(t)
where n is the order of Q(D). If the order of P(D) is less than the order of Q(D), then b_n = 0, and the impulses term b_nδ(t) in h(t) is zero. (This is usually the case.)
Example 2: Find the impulse response function for the system specified by the equation (D² + 3D + 2)y(t) = Df(t).




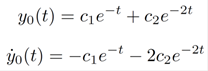
Initial condition:



Leads to





So



To find the impulse response, need





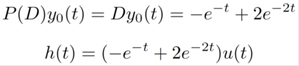
Example 3: RLC circuit, f(t) = 10e^-3tu(t), y(0) = 0, v_C(0) = 5.
Zero input current is





Impulse response (from before): h(t) = (2e^-2t – e^-t)u(t). Output:
y(t) = f(t) * h(t) = 10e^-3tu(t) * (2e^-2t – e^-t)u(t) = 10e^-3tu(t) * 2e^-2tu(t) – 10e^-3tu(t) * e^-tu(t)
Using the table,



Then the total response is
y_tot(t)= -5e^-t + 5e^-2t + (-5e^-t + 20e^-2t – 15e^-3t) t≥0
Now there is another way of looking at this: Observe that some of the output terms are due to the natural modes of the system, while others are due strictly to the input. The terms due to the natural modes of the system are referred to as the natural response, while the terms due to the input are referred to as the forced response.




Graphical convolution. What is happening in the convolution integral? Can we understand it better? Look at




First, flip g(τ). Then shift this by t. Take the product and integrate. Show some pictures. Do the pulse with the pulse. Do e^-tu(t) with e^-2tu(t).
Observe where the width property comes from.
Now comment on where this thing comes from again: the initial signals goes through first, then the next, and so forth. Because of the way we draw things, we have to flip the input around.