CONCEPTS OF METERING ELECTRICITY

previous ELECTRIC METERING

To effectively manage or participate in electric energy management programs, a basic knowledge of electricity and meters is highly beneficial. A course in electricity and meters is beyond the scope of this manual. The material presented here acquaints individuals with fundamental electrical units and phenomena specifically related to meters. The major emphasis is to show how information obtained from electrical meters is applicable to management programs. There is some mathematical and technical discussion, but it has been kept to a basic level.

COMMON METERING TERMS: The following definitions provide the means for a basic application of metering data.

Ampere (I): Unit of current or rate of flow of electricity.

Blondel’s Theorem: The power/energy in a circuit of N lines can be metered by N single-phase watt/watthour meters with the potential circuits connected from each line to any common point. If the common point is on one of the lines, the power/energy can be metered by N-1 watt/watthour meters.

Demand Analysis: Demand analysis is the critical examination of demand profiles obtained from a power survey recorder (PSR), or compiled from data collected using kilowatthour meters, rate schedules, demand registers, and other instruments. One of its purposes is to locate peaks and valleys in a demand profile to evaluate the possibility of load shifting to level out the profile and to reduce demand charges.

Demand Factor: Ratio of maximum demand to the total connected load.

Demand Peaks: Although demand billing procedures are not uniform, time-dependent demand charges are typical. One method uses onpeak, midpeak, and offpeak hours to assess demand charges. Although hours may vary between summer and winter months, a typical summer schedule is: onpeak-demand--l:00 PM to 7:00 PM, weekdays; midpeak-demand--9:00AM to 1:00 PM and 7:00 PM to 11:00 PM, weekdays; offpeak-demand--all other hours including holidays. Highest charges are assessed for onpeak-demand with proportional cost reductions for midpeak and offpeak periods.

Demand Profile: A demand profile is a graphic representation of electrical demand made on a system during a given period. The profile illustrates the relationship between demand, in kilowatt, and time of day demand occurred. When graphing, place demand on y-axis and time on x-axis.

Diversity Factor: Ratio of the sum of individual maximum demands of various subdivisions of a system to the maximum demand of the whole system.

Horsepower (hp): Measure of time rate of doing work; equivalent to raising 33,000 lbs, one ft in one minute; 746 watts.

Hours-Midpeak: This is time-of-day charge used by some utilities in demand or total energy billing. Midpeak-hour demand charges are often considerably less than onpeak-hour demand charges. Total energy charges my average 15 to 20 percent less than onpeak-hour charges. Although the schedule will vary among utilities , a typical summer schedule for midpeak-hours is from 9:00 AM to 1:00 PM and 7:00 PM to 11:00 PM on weekdays.

Hours-Offpeak: This is a time-of-day charge used by some utilities in demand or total energy billing. Use of electricity during offpeak-hours results in lowest total energy charges and in some instances may not result in a demand charge. Although schedules will vary, a typical summer offpeak-hours schedule is all holidays, Saturdays, Sundays, and from the hours of 11:00 PM to 9:00 AM on weekdays.

Hours-Onpeak: This is a time-of-day charge used by some utilities in demand or total energy billing. Use of electricity during onpeak-hours results in the highest charges for demand or total energy use. Although hours may vary among utilities and will vary between summer and winter, a typical summer schedule for onpeak-hours demand is from 1:00 PM to 7:00 PM on weekdays.

Kilovolt Amperes (kVA): 1,000 volt-amperes.
Kilowatt (kW): 1,000 watts.
Kilowatthour (kWh): 1,000 watthours.
Load Factor: Ratio of average load over a designated period of time to peak load occurring in that period.
Load Shedding: Load shedding is shutting down electrical loads to reduce total load and to lower demand.
Megohm: 1,000,000 ohms.
Ohm (R): unit of resistance.
Ohm’s Law: I = E/R (cd or 100% pf)

Phase Angle: The phase angle refers to the angle created between the sinusoidal voltage curve and either a lagging or leading current curve. Although current may either lag or lead voltage, commercial users try to ensure current is slightly lagging.

Power Factor: Power factor (pf) is a ratio of real power measured in watts of an alternating current circuit, to apparent power measured in voltamperes. Power factor is also the cosine of the phase angle between the voltage and current.

Power-Apparent: Apparent power is the product of voltage and current in a circuit in which voltage and current reach their peaks at different times. In other words, there is a phase angle between the voltage and current. Apparent power is measured in volt-amperes.

Power-Reactive: Reactive power, also called wattless power, is measured in terms of voltampere-reactive (VAR). Reactive power increases as power factor decreases and is the component of apparent power that does no real work in the system.

Power-Real: Real power is the component of apparent power that represents true work in an alternating current circuit. It is expressed in watts and is equal to apparent power times power factor.

Signal-Analog: An analog signal is a voltage or current signal that is a continuous function of the measured parameter. Analog signals provide direct, instantaneous information. It is most often used for onsite monitoring with meters and pen chart recorders. If analog signals are to be transmitted over long distances, the signal is generally converted into a numerical value before transmission.

Signal-Digital: A digital signal (numerical display) is pulse generated and discrete. Systems used for transmission are RS-232, 4-20 ma, and 1-10 volt.

Time-of-Use Charges: Many utilities adjust energy charges for the time-of-day or time-of-year that energy is used. For time-of-day billing, onpeak energy costs will be higher than midpeak and offpeak costs. Other utilities have established winter and summer rates.

Volt (E or V): Unit of electromotive force.

Volt Amperes (VA): Unit of apparent power; EI (single phase); E x I x 1.73 (3 phase).

Watt (W): Unit of true or real power; VA x p-f.

ELECTRIC METERS AND BILLING: In charging for electric energy, utility companies use three types of meters. These are demand, power factor, and watthour meters. Total energy charges are obtained from a watthour meter, power factor from a power factor meter, and demand values from a demand meter. Typically, watthour and demand meters are combined.

1. Total Energy Charges: The total energy used on an installation is recorded on watthour meters and is billed in kilowatthours. The greater the wattage of electrical devices, the higher the charges for total energy. Any method that reduces the time of operation or the power used by an electrical device will result in decreased energy charges. Many manufacturers now produce products that use significantly less energy, but perform essentially the same tasks as higher powered equipment.

2. Power Factor: Power factor occurs only in AC circuits and is defined as the ratio of real power to apparent power. Power factor is also the cosine of the phase angle between the voltage and current signals. Figure 9-1 provides a graphic representation of power factor. When the current signal crosses the x-axis after the voltage signal, the power factor is said to be lagging. If it crosses the x-axis before the voltage signal, the power factor is leading. Power factor values can range from leading 0.2 to lagging 0.2, with an optimum value of 1. Typically power factor ranges from between 0.75 and 0.95, lagging.

2.1 Apparent Real, and Reactive, Power: Real power is actual power used by a piece of equipment and converted ultimately into work. Reactive power is not converted into work but is a measure of the stored energy (either capacitive or inductive) that must be constantly transferred between the source of power and the end equipment. Motors require reactive power to magnetize their coils. For each sinusoidal cycle of the voltage provided to the motor, the magnetic field builds up and collapses. Reactive power Is borrowed as the magnetic field is built up and, as the magnetic field collapses, the power is returned. Apparent power is power a utility must generate to operate the equipment. It contains components of both real and reactive power as shown on the bottom of Figure 9-1. If the power factor is equal to 1 (voltage and current signals coincide), then real and apparent power are equal. However, because of the power factor effect, the utility must generate a greater amount of power than required by online equipment for useful work. Since apparent power is defined as volts times amps, this requires the utility to generate more current. In addition to costing more money, the increased amperage flowing through transmission lines and into the equipment causes both to heat, which hastens deterioration and adversely affects regulation in transformers. Since reactive power does not register on watthour meters but results in added expense to the utility, the added cost is passed on to the customer in the form of a power factor charge.

3 Demand: Demand is defined as average power used during some utility-selected time period. Power is usually expressed in kilowatts and normal industry standards for time are 15- or 30-minute intervals, but occasionally are as long as 60 minutes. In Figure 9-2, a 15-minute time interval from 0900 to 0915 is used to illustrate demand. During this interval load varies as shown: 300 kW for the first 5 minutes, 400 kW for the next 5 minutes, and 800 kW for the last 5 minutes. The average power used during this 15-minute period is 500 kW, shown as a dotted line. This dotted line is “demand value” or simply "demand” for that 15-minute interval. Note that the area under the dotted line (demand) is exactly equal to the area under the solid line (varying load). This leads to yet another definition of demand. Demand is that value of power which, if held constant over the interval, will account for the same consumption of energy as the real power. Figure 9-3 is an actual demand graph over four time intervals. As before, demand for each time interval is shown by the dotted line with actual power consumed represented by the solid line. Again for each interval, area under the dotted line is equal to area under the solid line. If demand shown in the second interval was the highest demand for the entire billing period, it would be called peak demand and would be the value used by utility companies for billing. Since demand billing varies so greatly among utilities, it is necessary to thoroughly research and understand the policies of the utility serving the facility. Almost without exception, demand will be the major element of any electrical bill. The energy manager must try to find ways to reduce peak demand so that demand can be as level as possible. Even though utilities must be capable of providing maximum power demands, it is not necessary to provide it at all times. This will result in a significant reduction in demand charges.

FIGURE 9-1. Alternating Current Power

FIGURE 9-2. Demand Calculation for One Time Interval

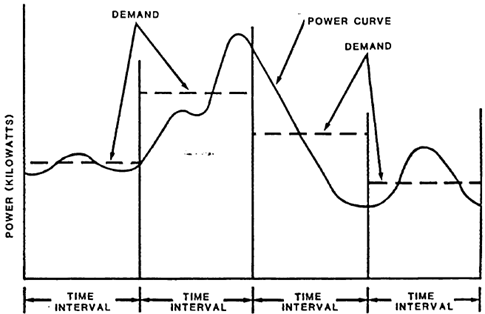FIGURE 9-3. Demand Chart

ELECTRIC METERING COMPONENTS: A wattmeter monitors the two basic components of electrical power, current and voltage. Typical connection diagrams for a voltmeter and ammeter are shown in Figure 9-4. The voltmeter is a high-resistance device and is always connected in parallel with a source of power or load. The ammeter measures-current flowing-through a conductor is a low-resistance device always connected in series with the source of power or load. The wattmeter is a combination of both voltmeters and ammeters. It measures power flow from the source to the load. The potential coils are connected in parallel and the current coils are connected in series with the load. Typical connections for a single phase wattmeter is also shown in Figure 9-4.

1. Watthour Meters: The watthour meter is a carefully calibrated induction motor. It measures electrical energy by utilizing the interaction of fluxes generated by current and voltage elements acting to produce eddy currents in the rotor (disk). The eddy current flow produces lines of force which in turn interact with the flux in the air gap to produce turning torque on the disk. The speed that the disk turns depends upon the energy (watts) being measured. Each revolution of the meter disk has a value in watt-hours. A constant (Kh) represents the number of watthours per revolution. A register counts revolutions and displays the count as kilowatthours (kWh).

FIGURE 9-4. Meter Connection Diagrams

POLYPHASE A-C CIRCUITS: The energy delivered over a polyphase circuit is the total energy delivered over each equivalent single-phase circuit that make up the polyphase circuit. Energy can be measured by connecting a single-phase watthour meter in each phase and then adding up readings of individual meters. This is not commercially practicable because: it requires too many meters; it takes much more time to read the meters; and it multiplies the chance of mistakes both in reading meters and in totaling meters. The electrical industry has developed polyphase watthour meters.

POLYPHASE WATTHOUR METER: The polyphase watthour meter is a combination of single-phase watthour meter stators that drive a rotor at a speed proportional to the total power in the circuit. The meter consists of a multistator motor, means for balancing the torques of all stators, a magnetic retarding system, a register, and compensating devices. These components are assembled on a frame and mounted on a base.

1. Operating Principle: The operating principle of polyphase watthour meters, having any number of stators, is the same as single-phase watthour meters. Torque on each stator results from current in one set of electromagnetic coils and eddy currents induced in a disk, or disks, by current in the other set of coils. The torques of the several stators combine to give a resultant torque proportional to total power.

2. Blondel’s Theorem: Because the same rules apply to measurement of both polyphase energy and polyphase power, principal parts of single-phase watthour meters can be combined for polyphase energy measurement, much as components of single-phase wattmeters are combined for polyphase power measurement. Blondel’s theorem applies to measurement of energy exactly as it does to measurement of power. A polyphase watthour meter is built with the number of elements necessary to satisfy Blondel’s theorem.

METER TYPES: A wide variety of meters are available to meet almost every measuring need. Meters can be divided into two major types, indicating and recording.

1. Indicating Meters: Indicating meters are used to provide a measured value at a given moment, and show how instantaneous value changes as a function of time. Indicating meters may have analog pointers or digital readouts. Some meters have a built-in time delay. Many are equipped to show average use over a 15 minute to 30 minute increment.

2. Recording Meters: Recording meters are used to accumulate a measured value over a period of time. These meters use either dials such as a kilowatthour q eter, a paper chart (either circular or strip), or magnetic tape where readings are coded into pulses and then encoded by a computer system to record the increase in reading between reading intervals.

next METERS AND SUPPORT DEVICES