MODELING A STABELIZATION FIXTURE WITH END PRESSURE USING SOLID ELEMENTS

previous MODELING A FRAME STRUCTURE (WEIGHT BENCH) USING BEAM ELEMENTS

MSC/PATRAN TUTORIAL # 5
MODELING A STABELIZATION FIXTURE WITH END PRESSURE USING SOLID ELEMENTS

I. THE PHYSICAL PROBLEM
The structure below is designed to support a bearing on its right, curved edge. A similar part exists to hold the bearing on the other side. The left edge is cantilevered or "built in". This means that both the translations and the rotations are held to zero along this edge. A pressure load of magnitude 100 lb/in2 in the negative X direction results from the bearing reaction. The material properties for the beam are E= 10 x 106 psi (typical for aluminum) and n = 0.3 . The part has a solid cross section with thickness in the Zdirection t = 3 in.

II. THINKING ABOUT THE MECHANICS
The analytic solution for stresses and displacements for this problem is not readily available. However, any Mechanics of Materials text will provide equations for the max stress and the max displacement of simple problems that will provide upper or lower bounds for stresses and displacements. These analytic verifications will be discussed below.

Some basic questions to consider before creating the computational model are:

1. Where will the stresses be tensile and where will they be compressive?
2. What will be the magnitude and direction of the reaction forces/moments?
3. Where will the stresses be zero?
4. How do the displacements vary along the length (linear, quadratic etc.)?
5. What will the local effect of the pressure load be on the stresses?
6. Is the model fully constrained from rigid body rotations and displacements?

Answering these questions qualitatively, along with the quantitative analytical solutions for the max stress and displacement will provide reinforcement that your computational model is correctly constructed.

III. CREATING THE GEOMETRIC AND FINITE ELEMENT MODEL
1. Create the Geometry
Create the 3-d object below according to the following steps:
Create the points shown with coordinates as in the table

Next create curves between points 1 and 2, 3 and another curve between 4, 6 and another curve between 7, 8 and 9, 2 and another curve between 8, 3 and 7.

Create the curve between points 2 and 3 and between points 7and 8 using the 2-d arc 2point using a radius of 1.
Create the arc between points 4, 5 and 6 using the 2d arc3point option.
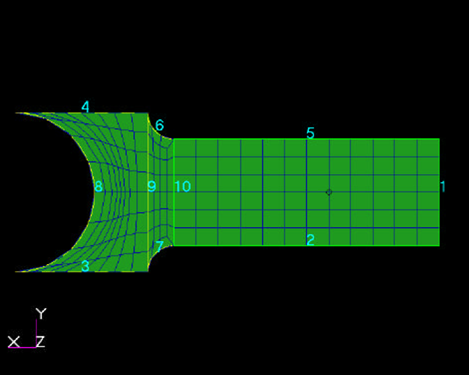
Now create 3 surfaces. The instructions will use the curve numbers in the picture below.
Please substitute the curve numbers form the curves you created.

Create the first surface between the curves 1,2,5 and 10 using the Create/Surface/Edge command.
Create the 2nd surface between the curves 7, 10, 6 and 9 and the 3rd surface between the curves 3, 9, 4, and 8.

Now create solids of thickness 3 (in the Z direction) from each of the 3 surfaces using the Create/Solid/Extrude command. The translation vector will need to be <0,0,3>.

When you are done, the part will look like this.

2. Create the Finite Element Mesh The first task is to seed the mesh. This is critical in this model as the model contains 3 separate solids which will need to be meshes separately. Then the nodes will need to be equivalenced so that the 3 solids are “attached” computationally. If this equivalencing is to work correctly, nodes along the interface between 2 solids will need to be coincident. The mesh seed will ensure this. Using the Create/Mesh Seed/Uniform option in the Element menu, create mesh seeds as shown below. Note that is your mesh seeds are a little different than the ones shown below, it will simply mean that you end up with a slightly different number and placement of elements. This should NOT affect the results of your analysis substantially except in one case. The distribution of elements in the Y direction must be constant across the part. For example if you have 6 elements across the far left edge, then you need to have 6 elements across the right curved edge and across other X=constant planes in the part. The reason this is important is that if the element pattern is not symmetric in the in the Y direction, the part will experience a nonsymmetric distribution of loads in the Y direction, resulting in non-physical displacements in the Y direction and also resulting in non-physical bending stresses.

Next place the actual mesh on the solids using the Create/Mesh/Solid. If the mesh seeds are done as shown, it will not matter what the global edge length is. Use the Hex8 elements. Use the isomesh mesh generator.

Next equivalence the nodes using the Equivalence/All/Tolerance cube command. The defaults tolerance is fine. This should indicate approximately 64 nodes were deleted. The graphics will show these nodes along the interface between the 3 solids.

The completed mesh should look approximately as shown below.

3. Create the BC and Loads
To clamp the left edge (edge away from the rounded bearing surface) use the Create/Displacement/Nodal command in the Loads/BC menu. Set all 3 displacements and all 3 rotations to zero and select apply to the left edge.

Next create the pressure load on the bearing surface by using the Create/Pressure/element Uniform command. Make sure the element target type is 3d. Choose a pressure of 100. To select the application surface (in the Select Application Surface) turn on the geometry button and then select the icon for “Face of a Solid” and choose the curved surface shown highlighted below. The BC and loads graphics will appear as shown.

The BC on the left and the pressure load on the right might look different on your part depending on whether you have applied the BC or pressure to the geometry.

4. Create the Material and Property
The material for the part is aluminum which has a E of 10e6 psi and a Poisson’s ratio of 0.3. Using the Materials menu create an isotropic homogeneous material with these properties.

The properties set is made using the command Create/3D/Solid in the properties menu. Input the properties simply as the material you just created. Select the entire part to have these properties.

5. Do the Analysis In the analysis menu, use the command Analyze/Entire Model/Full Run . Set the Translation Parameters to output the *.op2 file. Read in the analysis results Using the command Read Output2/Result Entities/ Translate. Select the appropriate results (*.op2) file.

6. View the Results
In the results menu, use the command Create/Quick Plot. Make plots of the displacements ad the appropriate stresses.

next MODELING A CANTILEVERED BEAM’S VIBRATION USING 4 NODE SHELL ELEMENTS