Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis: DC-AC CONVERTERS

Showing posts with label DC-AC CONVERTERS. Show all posts

Three-Phase Inverter

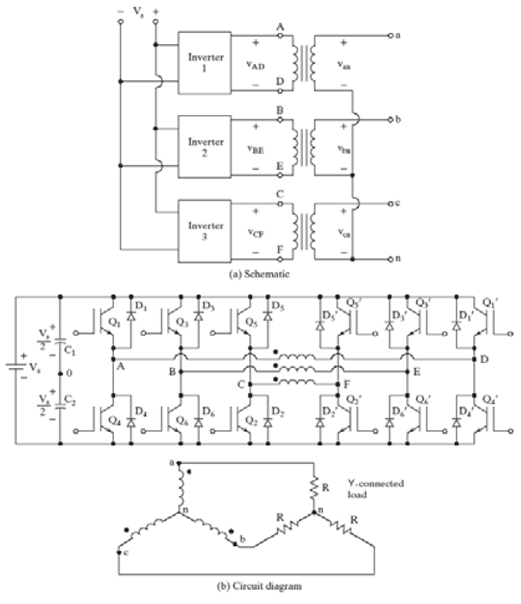
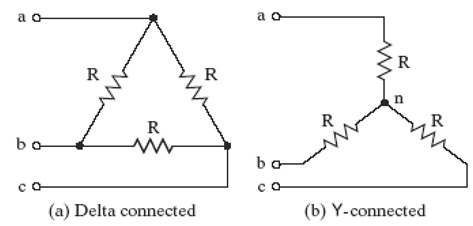
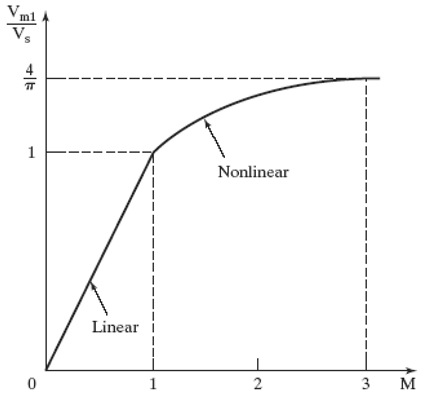
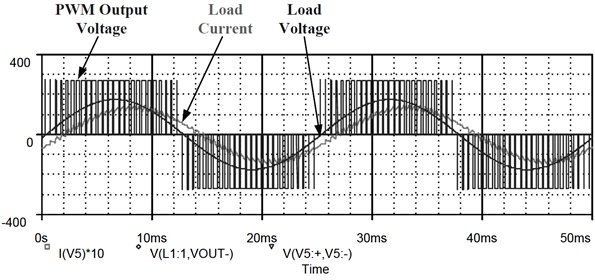
Used to supply three-phase loads
Three single-phase inverters could be used, however, 12 switches are necessary, as a result, less efficient
Consists of three legs, one for each phase
One of the two switches in a leg is always ON at any instant
Output of each leg depends on Vs and the switching status

Three-Phase PWM Inverter

${v_{ab}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t + \frac{\pi }{6})}$

${v_{bc}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t - \frac{\pi }{2})}$

${v_{ca}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t - \frac{{7\pi }}{6})}$

$\begin{array}{l} {V_{Ln(rms)}} = \frac{{4{V_S}}}{{\sqrt 2 n\pi }}\sin (\frac{{n\pi }}{3})\\ {V_{L1(rms)}} = \frac{{4{V_S}}}{{\sqrt 2 \pi }}\sin (\frac{\pi }{3}) = 0.7797{V_S} \end{array}$

power electronic converter: DC-AC CONVERTERS

Delta and Y-Connected

Equivalent Circuits

Equivalent Circuits for Y-Load

${v_{ab}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{\sqrt 3 n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t)}$

${v_{bc}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{\sqrt 3 n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t - \frac{{2\pi }}{3})}$

${v_{ca}}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{\sqrt 3 n\pi }}\sin (\frac{{n\pi }}{3})\sin n(\omega t - \frac{{4\pi }}{3})}$

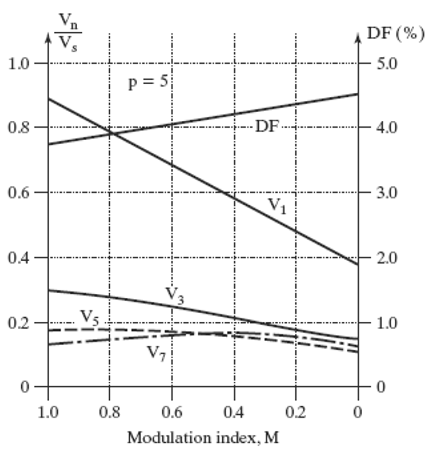
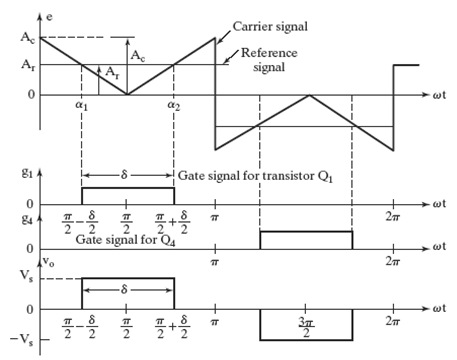
previous Sinusoidal PWM

next Sinusoidal PWM 3-Phase Inverter

Sinusoidal PWM

${d_m} = \frac{{{\delta _m}}}{\omega } = {t_{m + 1}} - {t_m}$

${V_{o(rms)}} = {V_S}\sqrt {\sum\limits_{m = 1}^{2p} {\frac{{{\delta _m}}}{\pi }} }$

${v_{o(t)}} = \sum\limits_{n = 1,3,5,..}^\infty {{B_n}\sin n\omega t}$

power electronic converter: Sinusoidal PWM

Harmonic Profile for p =5

${B_n} = \sum\limits_{m = 1}^{2p} {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{n{\delta _m}}}{4}}$ $\left[ {\sin n\left( {{\alpha _m} + \frac{{3{\delta _m}}}{4}} \right) - \sin n\left( {\pi + {\alpha _m} + \frac{{3{\delta _m}}}{4}} \right)} \right]$
Peak Fundamental versus M

previous Voltage Source SPWM Inverter
next Three-Phase Inverter

Voltage Source SPWM Inverter

During the positive cycle, S1 and S2 are switched by the high frequency pulse train shown in Figure (next slide). During the negative cycle, the pulse train switches S3 and S4. The load inductance integrates the generated pulse train and produces a sinusoidal voltage (V_ac) and current wave, as shown in the next Figure. The width of each pulse is varied in proportion to the amplitude of a sine wave. A typical PWM waveform is shown in the previous slide. The switches in this converter are controlled by gate pulses. The gate signal contains several pulses distributed along the half-cycle. The control circuit produces the gate pulse train by generation of a triangular carrier wave and a sinusoidal reference signal. The two signals are compared, and when the carrier wave is larger than the reference signal, the gate signal is positive. When the carrier wave is smaller than the reference signal, the gate signal is zero. This results in a gate pulse with variable width.

Figure: Single-phase voltage source converter.

Figure: Gate pulse input signal, and ac voltage and current outputs of a pulse width modulation (PWM) converter.

(a) Triangular carrier wave and sinusoidal reference signal

(b) Variable-width gate pulse signal

Figure: Pulse width modulation (PWM) signals.

Figure (a) shows the carrier wave and reference sine wave; (b) depicts the resulting gate signal with variable width pulses. It has to be noted that several other methods are used for generation of PWM signals as discussed earlier.

The frequency of the reference sine wave determines the frequency of the generated ac voltage. The amplitude of the ac voltage can be regulated by the variation of the reference signal amplitude. The amplitude of the fundamental component of the ac voltage is:

$\begin{array}{l} {V_{ac}} = \frac{{{V_{control}}}}{{{V_{carrier}}}}{V_{dc}} = m{V_{dc}}\\ or\\ {V_{om1}} = \frac{{{A_r}}}{{{A_c}}}{V_S} = M{V_S} \end{array}$

The modulation index (m or M) is the ratio of the peak-to-peak ac voltage (2Vac) to the dc voltage.

Freewheeling diode

The inverter interrupts the current several times each cycle. The interruption of an inductive current would generate unacceptably high overvoltage. This over voltage generation is eliminated by providing freewheeling diodes connected in parallel with the switches.

previous Multiple-Pulse PWM
next Sinusoidal PWM

Multiple-Pulse PWM

$d = \frac{\delta }{\omega } = {t_{m + 1}} - {t_m}$

$= M{T_S} = M\frac{T}{{2p}}$

${V_{o(rms)}} = \sqrt {\frac{{2p}}{{2\pi }}\int_{(\pi /p - \delta )/2}^{(\pi /p + \delta )/2} {V_S^2d\theta } }$

$= {V_S}\sqrt {\frac{{p\delta }}{\pi }}$

${v_o}(t) = \sum\limits_{n = 1,3,5,...}^\infty {{B_n}\sin n\omega t}$

power electronic converter-Multiple-Pulse PWM

Harmonic Profile for p =5

${v_o}(t) = \sum\limits_{n = 1,3,5,...}^\infty {{B_n}\sin n\omega t}$

${B_n} = \sum\limits_{m = 1}^{2p} {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{n\delta }}{4}}$ $\left[ {\sin n\left( {{\alpha _m} + \frac{{3\delta }}{4}} \right) - \sin n\left( {\pi + {\alpha _m} + \frac{\delta }{4}} \right)} \right]$
previous PWM Inverters
next Voltage Source SPWM Inverter

PWM Inverters

Pulse Width Modulation (PWM)

The amplitude of the harmonics can be reduced by using the pulse width modulation (PWM) technique.
The basic concept of the PWM method is the division of the on-time into several on and off periods with varying duration.
The rms value of the ac voltage is controlled by the on-time of the switches.
The most frequently used PWM technique is sinusoidal pulse width modulation (SPWM).

Types of Pulse Width Modulation (PWM)

Single-pulse-width modulation
Multiple-pulse-width modulation
Sinusoidal pulse-width modulation
Modified sinusoidal pulse-width modulation
Phase-displacement control

Single-Pulse PWM
Duty ratio D is given by
$\begin{array}{l} D = \frac{\delta }{\pi }\\ or\\ \delta = D\pi \end{array}$
Pulse duration
$D = \frac{\delta }{\omega } = {t_2} - {t_1}$
$= M{T_S} = M\frac{T}{2}$
${v_o}(t) = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{n\delta }}{2}\sin n\omega t}$
${v_{o(rms)}} = \sqrt {\frac{2}{{2\pi }}\int_{(\pi - \delta /2)}^{(\pi + \delta /2)} {V_S^2d\theta } } = {V_S}\sqrt {\frac{\delta }{\pi }}$

power-electronic-converter-Single-Pulse PWM

Harmonic Profile for p =1

Example 1

A pulse width modulated single phase full-bridge inverter has a dc input of 240V. The inverter is operating at a duty cycle of 60% with a frequency of 5kHz. Determine-

the rms value of the ac output voltage, [185.9V]
the rms value of the fundamental frequency component of the output ac voltage [174.74V]
the rms value of the total harmonic component of the output voltage. [63.44V]

Example 2

A full-bridge PWM inverter operates from a 200V dc bus. The instantaneous output voltage v can be expressed using Fourier series as

$v = \sum\limits_{n = 1,3,5,..}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin \frac{{nD\pi }}{2}\cos n(\omega t - \frac{{D\pi }}{2})}$
Determine

The duty cycle that will totally eliminate the third harmonic. [D = 2/3]
What will be the rms values of the total output voltage and the fundamental frequency voltage as well as THD at the duty cycle in (a). [V_rms = 163.3V, V_1,rms = 155.88V]

previous Single-Phase Bridge Inverter
next Multiple-Pulse PWM

Single-Phase Bridge Inverter

In this circuit four switches are used and the DC supply centre-tap is not required. Switches Q1 and Q2 are switched together while switches Q3 and Q4 are switched together alternately to Q1 and Q2 in a complementary manner. The four feedback diodes D1-D4 conduct currents as indicated in the figure below.

The output load voltage alternates between +Vs when Q1 and Q2 are on and -Vs when Q3 and Q4 are on, irrespective of the direction of current flow. It is assumed that the load current does not become discontinuous at any time. In the following analysis we assume that the load current does not become discontinuous at any time, same as for the half-bridge circuit.

The output RMS voltage

${V_{o(rms)}} = \sqrt {\frac{2}{\pi }\int_0^\pi {V_S^2d\theta } } = {V_S}$

The fundamental RMS output voltage obtained from

${V_{o1(rms)}} = \frac{{4{V_S}}}{{\sqrt 2 \pi }} = 0.90{V_S}$

Fourier series of output voltage

${v_o}(t) = \sum\limits_{n = 1,3,5,....}^\infty {\frac{{4{V_S}}}{{n\pi }}} \sin n\omega t$

$= 0{\rm{ }}for{\rm{ }}n = 2,4,...$

Bridge inverters are preferred over other arrangements in higher power ratings
With the same dc input voltage, output voltage is twice that of the half-bridge inverter

Example-1
A single-phase half-bridge inverter has a dc input voltage of Vs = 440V.
Determine-
(a) The rms output voltage at the fundamental frequency, V1 [ V1,rms=198.07V]
(b) The harmonic factor of the lowest-order harmonic. [HF = 0.333]
Example-2
R=10, L=31.5 mH, C=112 µF, f₀=60 Hz, V_s=220 V, ω= 2πf= 377 rad/s,
X_L=jnωL= j11.87 nΩ, X_c= j/nωc = (-j23.68)/n Ω
$\left| {{Z_n}} \right| = \sqrt {{R^2} + {{\left( {n\omega L - \frac{1}{{n\omega C}}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {11.87n - \frac{{23.68}}{n}} \right)}^2}}$
${\theta _n} = {\tan ^{ - 1}}\left( {\frac{{11.87n}}{{10}} - \frac{{23.68}}{{10n}}} \right)$
${v_o}(t) = \sum\limits_{n - 1,3,5,...}^\infty {\frac{{4{V_S}}}{{n\pi }}\sin n\omega t}$
$= 0{\rm{ }}for{\rm{ }}n = 2,4,...$
${i_o}(t) = \frac{{{v_o}(t)}}{{\left| {{Z_n}} \right|\angle {\theta _n}}}$
$= \sum\limits_{n = 1,3,5,...}^\infty {\frac{{4{V_S}}}{{n\pi \sqrt {{R^2} + {{\left( {n\omega L - \frac{1}{{n\omega C}}} \right)}^2}} }}\sin (n\omega t - {\theta _n})}$

Power electronic converter-DC-AC CONVERTERS-Single-Phase Bridge Inverter

previous Performance Parameters of Inverters
next PWM Inverters

Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis

Power Semiconductor Devices

Latest Post