Power, Electronic Systems, Applications and Resources on Electrical and Electronic Project-Thesis: DC-DC CONVERTERS

Showing posts with label DC-DC CONVERTERS. Show all posts

DC-DC converters with electrical isolation

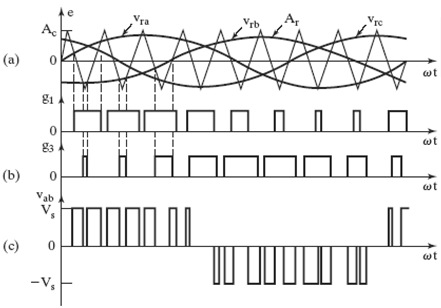
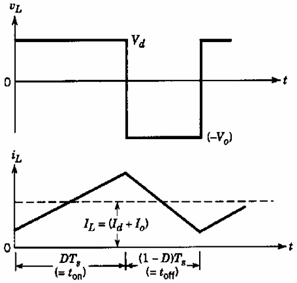
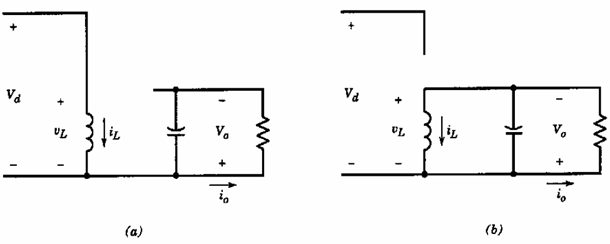
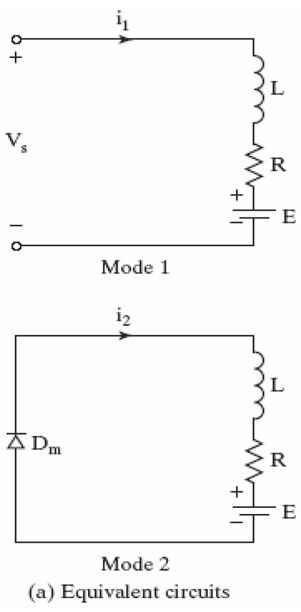
Transformer core characteristic:

Two basic categories of DC-DC converters with electrical isolation, based on the way of utilization of the transformer core:

Unidirectional core excitation: only the positive part (quadrant I) of the B-H loop is used.
Bidirectional core excitation: both the positive (quadrant I) and the negative (quadrant III) parts of the B-H loop are used alternatively.

Hence, DC-DC converters that constitute a switching DC power supply can be:
Transformer core characteristic

Unidirectional Core excitation DC-DC converters

Flyback converter (derived from buck-boost converter)
Forward converter (derived from buck converter)

Bidirectional Core excitation DC-DC converters

Push-pull converter (derived from buck converter)
Half-bridge converter (derived from buck converter)
Full-bridge converter (derived from buck converter)

Control of DC-DC converters with isolation

Flyback and forward converters
Push-pull, half-bridge and full-bridge DC-DC converters
Resonant DC-DC converters

previous Switching Power Supplies-Overview
next Flyback Converters

Sinusoidal PWM 3-Phase Inverter

Dc-to-ac converters are known as inverters. The function of an inverter is to change the dc input voltage to an ac output voltage of desired magnitude and frequency. The output voltage waveforms of ideal inverters should be sinusoidal. However, the output of practical inverters contains harmonics. For high power applications, low distorted sinusoidal waveforms are required. Harmonic contents could be minimized by the use of high-speed. semiconductor switching techniques

Inverters are widely used in industrial applications-

motor drives, UPS, induction heating, standby power supplies, etc.

input may be a battery, fuel cell, solar cell, or there dc source

Dc-to-ac inverters can make smooth transition into the rectification mode, where the flow of power reverses from the ac side to the dc side. Two types of inverters: single-phase inverters and three-phase inverters.

$n = j{m_f} \pm k$

$j = 1,3,5,...{\rm{ }}for{\rm{ }}k = 2,4,6,...$

$j = 2,4,6,...{\rm{ }}for{\rm{ }}k = 1,5,7,...$

${\hat v_{ab1}} = M\sqrt 3 \frac{{{V_S}}}{2}{\rm{ }}for{\rm{ 0}} \le {\rm{m}} \le {\rm{1}}$

power-electronic-converter-DC-AC CONVERTERS

previous Three-Phase Inverter

Step-Down/Step-Up (Buck-Boost) Converter

This converter can be obtained by the cascade connection of two converters: the step-down converter and the step-up converter
The output voltage can be higher or lower than the input voltage
Used in regulated dc power supplies where a negative polarity output may be desired with respect to the common terminal of the input voltage
The output to input voltage conversion ratio
$\frac{{{V_0}}}{{{V_d}}} = D\frac{1}{{1 - D}}{\rm{ k = D = duty ratio}}$
This allows V₀ to be higher or lower than V_d
When the switch is ON:
Diode is reversed biased
Output circuit is thus isolated
Inductor is charged
When the switch is OFF:
the output stage received energy from the inductor

Continuous current conduction mode

Inductor current i_L flows continuously
Average inductor voltage over a time period must be zero
Assuming a lossless circuit
Depending on the duty ratio, the output voltage can be either higher or lower than the input

Effect of parasitic elements

Parasitic elements are due to the losses associated with the inductor, capacitor, switch and diode
Parasitic elements have significant impact on the voltage transfer ratio

Example 2: Step-down (Buck) converter

The chopper below controls a dc machine with an armature inductance L_a = 0.2 mH. The armature resistance can be neglected. The armature current is 5 A. f_s = 30 kHz. D = 0.8

The output voltage, V_o, equals 200V.
(a) Calculate the input voltage, V_d
(b) Find the ripple in the armature current.
(c) Calculate the maximum and the minimum value of the armature current
(d) Sketch the armature current, i_a(t), and the dc current, i_d(t).

Example 3: Step-down (Buck) converter characteristics

A step-down dc-dc converter shown in the following figure is to be analyzed.

Assume in all calculations constant voltage over the series resistor R. The output capacitor C is large; assume no ripple in the output voltage. Rated output is 20 V and 25 A
(a) Calculate rated output power.
(b) Calculate equivalent load resistance.
(c) Calculate duty ratio D for rated output. The voltage across the series resistor R must be taken into consideration.

Example 4: Step-up (Boost) converter characteristics

A step-up dc-dc converter shown in the following figure is to be analyzed.

The input voltage V_d = 14 V.
The output voltage V₀ = 42 V.
Inductor L = 10 mH
Output resistor R = 1 Ω
Switching frequency f_s=10 kHz
(a) Duty ratio, switch on and off time.
(b) Plot inductor and diode voltages.

Step-up (Boost) converter characteristics

Comparison of Converters

Buck converter: step-down, has one switch, simple, high efficiency greater than 90%, provides one polarity output voltage and unidirectional output current

Boost converter: step-up, has one switch, simple, high efficiency, provides one polarity output voltage and unidirectional output current, requires a larger filter capacitor and a larger inductor than those of a buck converter

Buck-boost converter: step-up/step-down, has one switch, simple, high efficiency, provides output voltage polarity reversal.

Previous Boost Regulators – analysis of switch open

next DC-AC CONVERTERS (INVERTERS)

Boost Regulators – analysis of switch open

Mode 2: switch open

Now the diode is forward biased, and circuit appears as shown in figure bellow.

${v_L} = {V_S} - {v_o} = L\frac{{di}}{{dt}}$

Observe that i=i_L, and solving for di_L/dt results in

$\frac{{d{i_L}}}{{dt}} = \frac{{{V_S} - {v_o}}}{L}$

Since we know v₀ is constant, we see again that the rate of change of current is constant! Therefore the current must change linearly while the switch is open. But does it increase or decrease, that is, is di_L/dt positive or negative?

Power electronic converter: Boost Regulators – analysis of switch open

The answer to that question depends on whether v_o is larger or smaller than V_s. So let’s see if we can relate v_o to V_s.

Relation between v₀ and V_s

Since current must change linearly while switch is open, we can write:

$\frac{{\Delta {i_L}}}{{\Delta t}} = \frac{{{V_S} - {v_o}}}{L}$

Consider peak-to-peak ripple current. It must be the negative as that given by mode 1 condition.

Now we have 2 different expressions for the peak-peak ripple current:

From mode 1 analysis:

$\Delta I = \frac{{{V_S}}}{L}\Delta t = \frac{{{V_S}}}{L}kT$

From mode 2 analysis:

$\Delta I = \frac{{ - ({V_S} - {v_o})}}{L}(T - kT)$

So equate them!

$\frac{{{V_S}}}{L}kT = \frac{{ - ({V_S} - {v_o})}}{L}(T - kT)$

Bring V_s to the left.

$\frac{{{V_S}}}{L}kT + \frac{{{V_S}}}{L}(T - kT) = \frac{{{v_o}}}{L}(T - kT)$

Multiply by L and collect like terms.

$\frac{{{V_S}}}{L}kT + \frac{{{V_S}}}{L}(T - kT) = \frac{{{v_o}}}{L}(T - kT)$

Express v_o

${v_o} = \frac{{{V_S}}}{{1 - k}}$

Consider the case of k=0. What does this mean in terms of the circuit? It means the moment when the switch opens is $t = 0 \to$ Is always open!

Now what happens as k increases from 0? v₀ gets larger $\to$ It BOOSTS the voltage!

What happens when k→0?

Theoretically, ${{\rm{v}}_0} \to \infty$ , as shown.

Practically, parasitic elements become influential, and the output voltage is unstable for values of k approaching 1.0.

Consideration of Power Transfer

Let’s replace the load in our circuit with a battery.

How to deliver power to the battery?

Without the chopping action, V_s must be greater than E for transferring power from V_s to E. But with the boost chopper circuit, we can transfer power even if V_s<E.

At Relation between v₀ and V_s we have

Replacing v_o by E:

$\Delta I = \frac{{ - ({V_S} - E)}}{L}(T - kT)$

ΔI is a positive number since it was defined that way for mode 1.
For this to be the case, V_s-E < 0.
For this to be the case, V_s < E.
So power transfer (positive current) occurs when source voltage is LESS than the battery voltage!

Previous Boost Regulators – analysis of switch closed
next Step-Down/Step-Up (Buck-Boost) Converter

Boost Regulators – analysis of switch closed

Mode 1: switch closed

Observe that diode anode (a) is at ground potential and so must be low with respect to the diode cathode (c).

Diode is reversed biased, and the circuit appears as shown to the right.

Power electronic converter-Boost Regulators – analysis of switch closed

So the rate of change of current is a constant! This means that the current increases linearly while the switch is closed.

Let Δt be the amount of time the switch is closed. Define ΔI as the peak-topeak ripple current.

Recalling switch closing time is t1=kT, we have…

previous Boost Regulators

next Boost Regulators –analysis of switch open

Boost Regulators

Two modes:

1. Mode 1: switch closed

2. Mode 2: switch open

Power electronic converter: boost regulators

Assumptions:

Steady-state conditions exist
Switching period is T; switch is closed for kT, open for (1-k)T
Inductor current never goes to 0
Capacitor is very large, since Cdv/dt=iL, and iL bounded, dv/dt must be small =>> v₀ is constant.

The switch is implemented by a PWM-transistor & IGBT/MOSFET circuit. So we get a periodic switching.

Mode 1: switch closed

Power electronic converter: boost regulators-mode 1

Mode 2: switch open

Power electronic converter: boost regulators-mode 2

Previous Buck Regulators

next Boost Regulators –analysis of switch closed

Buck Regulators

Two modes:

1. Mode 1: switch closed

2. Mode 2: switch open

Power Electronic Converter: Buck Regulators

Mode 1: switch closed, i=i₁

${V_s} = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

Mode 2: switch open, i=i₂

$0 = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

Power Electronic Converter: Buck Regulators-mode

Mode 1:

For i=i₁

${V_s} = R{i_1} + L\frac{{d{i_1}}}{{dt}} + E$

${V_s} - E = R{i_1} + L\frac{{d{i_1}}}{{dt}}$

Laplace Transform

$\frac{{{V_s} - E}}{s} = R{I_1}(s) + Ls{I_1}(s)$

$\frac{{{V_s} - E + Ls{i_1}(0)}}{s} = {I_1}(s)(R + Ls)$

${I_1}(s) = \frac{{{V_s} - E + Ls{i_1}(0)}}{{s(R + Ls)}}$

Partial Fraction Expansion

${I_1}(s) = \frac{{{V_s} - E + Ls{i_1}(0)}}{{s(R + Ls)}} = \frac{{{V_s} - E + Ls{i_1}(0)}}{{sL(s + R/L)}}$

$= \frac{{\frac{{{V_s}}}{L} - \frac{E}{L} + s{i_1}(0)}}{{s(s + R/L)}}$

$= \frac{{{V_s} - E}}{{sR}} - \frac{{{V_s} - E - R{i_1}(0)}}{{R(s + R/L)}}$

Inverse Laplace Transform

${i_1}(t) = \frac{{{V_s} - E}}{R} - \frac{{{V_s} - E}}{R}{e^{ - tR/L}} + {i_1}(0){e^{ - tR/L}}$

Rearrange to get-

${i_1}(t) = {i_1}(0){e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

Use initial cdt: I₁=i₁(0)

${i_1}(t) = {I_1}{e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

Design features of Buck Regulator

Good design requires load time constant > switching time and τ=L/R > T
τ : time required to reach 63.2% of final value.
When τ<T, we see the full exponential change in i
When τ>T, we see just a part of the exponential change in i before the switch, and so we assume that I increases/decreases linearly between switching times
Ex: T=.001sec; L=7.5mH, R=5Ω and τ=L/R=.0015sec

Equivalent circuits and waveforms

Figure: Equivalent circuits and waveforms for RL loads.

But what is I1, I2?

Let’s look at previous equations for i₁ and i₂

From Mode 1 current expression & “boundary” condition at switching

${i_1}(t) = {I_1}{e^{ - tR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - tR/L}})$

We have

${i_1}(t = {t_1} = kT) \equiv {I_2}$

$\Rightarrow {I_2} = {i_1}(t = kT) = {I_1}{e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$ (5.15)

From Mode 2 current expression & “boundary” condition at switching

${i_2}(t) = {I_2}{e^{ - tR/L}} - \frac{E}{R}(1 - {e^{ - tR/L}})$

We have ${i_2}(t = {t_2}) = {I_3}$ and also note ${t_2} = (1 - k)T$

$\Rightarrow {I_3} = {i_2}(t = (1 - k)T) = {I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})$ (5.16)

From previous elastration, observe that, in steady-state, I₃=I₁….

$\Rightarrow {I_1} = {i_2}(t = (1 - k)T) = {I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})$ (5.16a)

Substitute (5.16a) into (5.15):

${I_2} = {i_1}(t = kT) = \left( {{I_2}{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})} \right){e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

Now solve for I₂

${I_2} = {I_2}{e^{ - (1 - k)TR/L}}{e^{ - kTR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}}){e^{ - kTR/L}} + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

$= {I_2}{e^{ - TR/L}} - \frac{E}{R}({e^{ - kTR/L}} - {e^{ - TR/L}}) + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

$\Rightarrow {I_2}(1 - {e^{ - TR/L}}) = - \frac{E}{R}({e^{ - kTR/L}} - {e^{ - TR/L}}) + \frac{{{V_s} - E}}{R}(1 - {e^{ - kTR/L}})$

${I_2} = - \frac{E}{R}\frac{{({e^{ - kTR/L}} - {e^{ - TR/L}})}}{{(1 - {e^{ - TR/L}})}} + \frac{{{V_s} - E}}{R}\frac{{(1 - {e^{ - kTR/L}})}}{{(1 - {e^{ - TR/L}})}}$

${I_2} = \frac{{[ - E{e^{ - kTR/L}} + E{e^{ - TR/L}} + {V_s} - E - {V_s}{e^{ - kTR/L}} + E{e^{ - kTR/L}}]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{\left[ {E{e^{ - TR/L}} + {V_s} - E - {V_s}{e^{ - kTR/L}}} \right]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{\left[ { - E(1 - {e^{ - TR/L}}) + {V_s}(1 - {e^{ - kTR/L}})} \right]}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{{E(1 - {e^{ - TR/L}})}}{{R(1 - {e^{ - TR/L}})}}$

$= \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{E}{R}$

${I_2} = \frac{{{V_s}(1 - {e^{ - kTR/L}})}}{{R(1 - {e^{ - TR/L}})}} - \frac{E}{R}$ (5.18)

Substitute eq. 5.18 into 5.16a:

${{I_1} = \left[ {\frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R}} \right]{e^{ - (1 - k)TR/L}} - \frac{E}{R}(1 - {e^{ - (1 - k)TR/L}})}$

$= \frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}}{e^{ - (1 - k)TR/L}} - \frac{E}{R}{e^{ - (1 - k)TR/L}} - \frac{E}{R} + \frac{E}{R}{e^{ - (1 - k)TR/L}})$

$= \frac{{{V_s}({e^{ - TR/L}} - {e^{ - (1 - k)TR/L}})}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R}$

$= \frac{{{V_s}(1 - {e^{kTR/L}})}}{{R(1 - {e^{TR/L}})}} - \frac{E}{R}$

$= \frac{{{V_s}({e^{kTR/L}} - 1)}}{{R({e^{TR/L}} - 1)}} - \frac{E}{R}$

Summary-

Define z=TR/L

${I_2} = \frac{{{V_s}({e^{ - kTR/L}} - 1)}}{{R({e^{ - TR/L}} - 1)}} - \frac{E}{R} \Leftarrow Eq.5.18 \Rightarrow {I_2} = \frac{{{V_s}({e^{ - kz}} - 1)}}{{R({e^{ - z}} - 1)}} - \frac{E}{R}$

${I_1} = \frac{{{V_s}({e^{kTR/L}} - 1)}}{{R({e^{TR/L}} - 1)}} - \frac{E}{R} \Leftarrow Eq.5.17 \Rightarrow {I_1} = \frac{{{V_s}({e^{kz}} - 1)}}{{R({e^z} - 1)}} - \frac{E}{R}$

What is z?

Recall τ =L/R is the time constant.
$\Rightarrow z = T/\tau$
So z is the ratio of chopping (or switching) period to load time constant.
Now let’s consider the peak-to-peak ripple current.

Figure: Equivalent circuits and waveforms for RL loads.

Therefore the peak-to-peak ripple current is given by

$\Delta I = {I_2} - {I_1}$

Plug in eq. 5.17 and 5.18 and will get:

$\Delta I = \frac{{{V_s}}}{R}\frac{{1 - {e^{ - kz}} + {e^{ - z}} - {e^{ - (1 - k)z}}}}{{1 - {e^{ - z}}}} - \frac{E}{R}......Eq.5.19$

It is interesting to identify the duty ratio for maximum ripple. To do this, differentiate eq 5.19 with respect to k and set to 0.

$\frac{d}{{dk}}\Delta I = \frac{d}{{dk}}\left\{ {\frac{{{V_s}}}{R}\frac{{1 - {e^{ - kz}} + {e^{ - z}} - {e^{ - (1 - k)z}}}}{{1 - {e^{ - z}}}} - \frac{E}{R}} \right\} = 0$