CONCEPTS OF METERING FLUID FLOW

previous DEVELOPING A METERING PROGRAM

Selection of the proper meter for measuring a flowing fluid (gas, steam, or liquid) is often a complicated process. Knowledge of certain fluid flow fundamentals will help in understanding the operating principles of various meters and assist in meter selection.

COMPRESSIBLE AND INCOMPRESSIBLE FLOWS: Flows in which variations in density are negligible are termed incompressible. Density of an incompressible fluid is not affected by changes in pressure and velocity. Flow rates of a compressible fluid are significantly affected by pressure and temperature changes. These characteristics must be considered when measuring the flow of fluids.

MEASURING FLUID FLOW: With most fluid flow measurement instruments, the flow rate is determined inferentially by measuring the fluid’s velocity or change in kinetic energy. Velocity depends on the pressure differential that is forcing the fluid through the pipe or conduit. Because the pipe’s cross-sectional area is constant, the average velocity is an indication of flow rate. The basic relationship for determining the fluid’s flow rate in such cases is:

Q = V x A
where:
Q = flow rate
V = average fluid velocity
A = cross-sectional area of pipe

The equation can be adjusted to determine volumetric, mass, and heat flow rates. For compressible fluids, pressure and/or temperature must be measured to determine the fluid density. This changing density must be used in the basic formula to determine a compensated flow rate.

1. Direct Measurement: Direct measurement of fluid flows are made using positive displacement meters. These units cannot meter steam or other high temperature gases. The flowing fluid is divided into specific measurable units and totalized using mechanical or electronic counters.

2. Indirect Measurement: Differential pressure and velocity flowmeters indirectly measure fluid flow rates. Many meters in use today operate on the differential pressure concept. Such meters use the correlation between pressure and velocity to determine the rate of flow. This correlation is expressed by the differential pressure formula which states that flow is proportional to the square root of the differential pressure, i.e.,

. For velocity meters the relationship of the continuity equation, Q = V x A, is applied. Velocity meters measure velocity at a point or full bore and calculate flow. A correction factor must be applied to these meters which results in accuracies of 95 to 99 percent.

3. Turndown Ratio: Turndown ratio, also known as rangability, is the ratio of the maximum flow rate a meter can accurately measure to the minimum flow that it can accurately measure.

4. viscosity: Viscosity, which influences meter selection, may be defined as the ease with which a fluid flows when it is acted upon by an external force. For example, water flows more rapidly from a container than heavy fuel oil. Under this condition, water is said to have a lower viscosity than fuel oil. An analogy for gases is somewhat more difficult to visualize, but it is sufficient to know that the viscosity of gases is extremely small compared to liquids. When a fluid flows through pipes, viscosity manifests itself as pressure losses and distortion of the velocity profile.

REYNOLDS NUMBER: The Reynolds Number describes whether a flow will be laminar or turbulent. The Reynolds Number is the ratio of inertia forces to viscous forces. This dimensionless ratio is expressed as:

where:
R = Reynolds number
P = fluid density
V = average pipeline velocity
D = inside pipe diameter
μ = fluid viscosity

Fluid viscosity and specific gravity are obtained from reference tables. Such tables are available from many sources. Engineering handbooks and manufacturer’s data are the most convenient sources.

1. Laminar and Turbulent Flow: The difference between a laminar and turbulent flow is shown in Figure 3-1. Laminar flow is described as a smooth flowing liquid. It flows in concentric layers around the center of the stream. The velocity is highest at the center and decreases to the outer edge of pipes. Laminar flow exists when the Reynolds number is approximately 2,000 or less. In applications with low velocity fluid flows or high viscosity media, the flow is usually laminar. If the Reynolds number is greater than approximately 3,000, the flow is assumed to be turbulent. Turbulent flow as contrasted with laminar flow consists of a large number of erratic eddy currents as shown in Figure 3-1. This results in a more uniform velocity profile from the center of the flow to the pipe than is found in a laminar flow; however, if the meter is not designed for this type of flow, its accuracy may suffer. Most applications involve Reynolds numbers above 3,000 due to either high velocity or low viscosity of the fluid. When flowing fluids have a Reynolds number between approximately 2,000 to 3,000, the flow type is unpredictable. This is known as the transition range and flow range may be either laminar, turbulent, or a combination. It should be recognized that the point where the flow characteristics change is an approximate number and the boundary values can vary significantly. The Reynolds number is important because of the impact it may have on final meter selection.

FIGURE 3-1. Laminar and Turbulent Flow Patterns

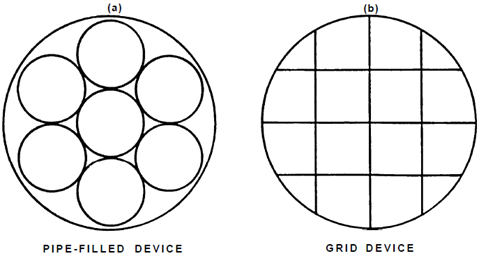
2. Nonstable Flow: A nonstable flow can be defined as a fluid that is swirling, pulsating, or changed in character by some projection into the fluid flow or a change in pipe direction. Most meters are designed to tolerate small amounts of nonstable flow and still register an accurate reading. To ensure the highest accuracy, all meters specify varying lengths of straight pipe before and after the meter. These lengths are usually expressed in multiples of pipe diameters. The required length of straight pipe is found by multiplying the pipe diameter by the multiple listed. Under some circumstances, it may not be possible to install meters with the recommended lengths of straight piping before and after the meters. If so, the flow distortions may exceed the ability of the meter to absorb and still return a reading with the required accuracy. If the velocity profile has been so distorted or swirl induced to such a degree that meter accuracy is compromised) installation of flow straighteners in the pipe run q ay correct the situation. Figure 3-2 shows cross-sections of two devices used to straighten fluid flows. Figure 3-2(a) is a section of pipe that is filled with straight tubes which will correct most types of distortions. Figure 3-2(b) is a similar device except that instead of tubes, a grid device assembled at 90 degree angles is inserted into the pipe. Some meters may also incorporate a short straightening device in the entrance section of the meter. Such meters usually have from 4 to 8 evenly spaced radial vanes just before the meter itself.

3 Effect on Installation. Since flow profiles in a pipe are not constant, meters must be correctly positioned during installation. Positioning is specific for each meter and is available from the meter manufacturer.